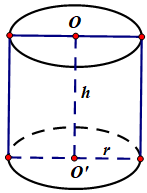
Người ta thiết kế một thùng chứa hình trụ có thể tích V cho trước. Biết rằng đơn giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và gấp  lần đơn giá của vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r. Tính tỉ số $\frac{h}{r}$sao cho chi phí vật liệu sản suất thùng là nhỏ nhất.

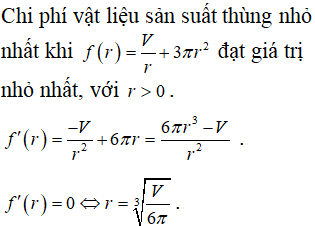
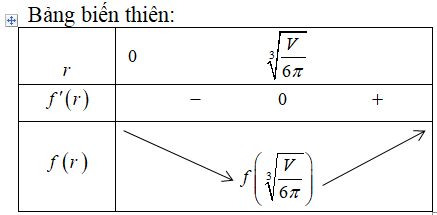
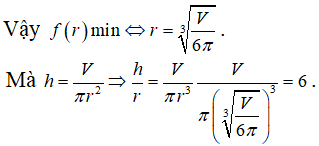
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D sao cho $AD=2\sqrt{3}a$ ; gọi C là hình chiếu vuông góc của D lên mặt phẳng chứa đường tròn (O’); trên đường tròn tâm O’ lấy điểm B (AB chéo với CD) . Đặt $\alpha$  là góc giữa AB và đáy. Tính $\tan \alpha$ khi thể tích khối tứ diện CDAB đạt giá trị lớn nhất.

Cho hình nón (N) có đỉnh O, góc ở đỉnh bằng 120^o, độ dài đường sinh bằng a. Mặt phẳng qua O cắt hình nón theo một thiết diện có diện tích lớn nhất bằng:

Cho hình nón có bán kính đáy bằng 3 chiều cao bằng 6, một khối trụ có bán kính đáy thay đổi nội tiếp khối nón đã cho (như hình vẽ). Thể tích lớn nhất của khối trụ bằng:

Một hình nón tròn xoay có đường sinh 2a. Thể tích lớn nhất của khối nón đó là:

Nam muốn xây một bình chứa hình trụ có thể tích 72m³ .Đáy làm bằng bêtông giá 100 nghìn đồng/m² thành làm bằng tôn giá 90 nghìn đồng/m² nắp bằng nhôm giá 140 nghìn đồng/m² .Vậy đáy của hình trụ có bán kính bằng bao nhiêu để chi phí xây dựng là thấp nhất?

Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B. Đặt $\alpha$ là góc giữa AB và đáy. Tính $\tan \alpha$ khi thể tích khối tứ diện OO’AB đạt giá trị lớn nhất.

Một công ty sản xuất một loại cốc giấy hình nón không nắp ( nghĩa là không có hình tròn đáy) có thể tích 27cm³. Với chiều cao h và bán kính đáy là r. Tìm r để lượng giấy tiêu thụ ít nhất:

Khi sản xuất vỏ lon sữa bò hình trụ có thể tích là V, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon sữa bò là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ bằng V và diện tích toàn phần hình trụ nhỏ nhất thì bán kính đáy bằng bao nhiêu?

Cho đường thẳng d cố định và một số thực dương a không đổi. Tập hợp các điểm M trong không gian sao cho khoảng cách từ M đến đường thẳng d bằng a là:

Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D trên đường tròn tâm O’ lấy điểm B, C sao cho AB//CD và AB không cắt OO’. Tính AD để thể tích khối chóp O’.ABCD đạt giá trị lớn nhất.

Cho hai mặt phẳng (P) và (Q) song song với nhau cắt khối cầu tâm O bán kính R tạo thành hai hình tròn (C₁) và (C₂) cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn, đáy trùng với hình tròn còn lại. Biết diện tích xung quanh của hình nón là lớn nhất, khi đó thể tích khối trụ có hai đáy là hai hình tròn (C₁)  và (C₂) bằng:

Chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có bán kính R là:

Cho hình trụ có bán kính đường tròn đáy là R, độ dài đường cao h. Kí hiệu S_tp là diện tích toàn phần của hình trụ và V là thể tích khối trụ. Trong các mệnh đề sau, mệnh đề nào đúng?

Gọi d là đường thẳng tùy ý đi qua điểm M(1;1) và có hệ số góc âm. Giả sử d cắt các trục Ox,Oy lần lượt tại A,B. Quay tam giác OAB quanh trục Oy thu được một khối tròn xoay có thể tích là V. Giá trị nhỏ nhất của V bằng:

Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là: