Trong không gian Oxyz, cho hai mặt phẳng -mx + 3y + 2z + m - 6 = 0 và -2x + (5m + 1)y + (m + 3)z - 10 = 0. Hai mặt phẳng này cắt nhau khi và chỉ khi:
A. m ≠ -4
B. m ≠ -6/5
C. m ≠ 1
D. Mọi m
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án C
Gọi hai mặt phẳng đã cho lần lượt là (P) và (Q). Ta có
![]()
Hai vectơ này song song khi và chỉ khi m - 6 -10 hay m -4 và tồn tại một số thực k sao cho
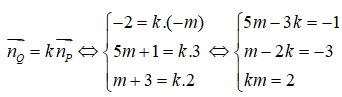
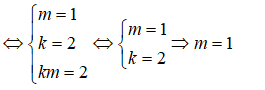 (thỏa mãn)
(thỏa mãn)
Từ đó suy ra hai mặt phẳng (P) và (Q) cắt nhau khi và chỉ khi hai vectơ pháp tuyến của chúng không song song, điều đó tương đương với m khác 1.
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua ba điểm A(1;0;1), B(0;-1;-3), C(2;1;3)
Trong không gian Oxyz, cho hai mặt phẳng song song (P): 4x - 3y - 8 = 0 và (Q): 8x - 6y - 1 = 0. Khoảng cách giữa hai mặt phẳng (P) và (Q) là:
Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x - y + 2z = 0; 2x - 2y + ( + 3m)z + - m = 0, trong đó m là tham số. Với những giá trị nào của m thì hai mặt phẳng (P) và (Q) song song?
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua hai điểm A(1;0;1), B(2;1;3), đồng thời vuông góc với mặt phẳng (Q): x + y - 3z = 0
Trong không gian Oxyz, cho hai vectơ = (-1; 3; 4), = (2; -1; 5). Tích có hướng của hai vectơ và là:
Trong không gian Oxyz, biết rằng trục Ox song song với mặt phẳng (P): y + z - 1 = 0. Khoảng cách giữa Ox và mặt phẳng (P) là:
Trong không gian Oxyz, tập hợp các điểm M cách đều hai mặt phẳng (P): 2x + 3y + z - 1 = 0 và (Q): 3x + y + 2z - 3 = 0 là hai mặt phẳng có phương trình là:
Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x + my + (m + 3)z + 1 = 0; x - y + 2z = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) vuông góc với mặt phẳng (Q)?
Trong không gian Oxyz, tập hợp các điểm M cách đều hai mặt phẳng tọa độ (Oxy) và (Oxz) là hai mặt phẳng có phương trình:
Trong không gian Oxyz, cho hai mặt phẳng: (P): x - 2y - 2z + 1 = 0, (Q): 2x - 4y - 4z + m = 0. Tìm các giá trị của m biết rằng khoảng cách giữa hai mặt phẳng (P) và (Q) bằng 1
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình 2x - 3y + (2m - 4)z + - m = 0, trong đó m là tham số. Với những giá trị nào của m thì (P) song song với trục Oz?
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2;1;3), vuông góc với mặt phẳng (Q): x + y - 3z = 0 đồng thời (P) song song với trục Oz
Trong không gian Oxyz, cho mặt phẳng (P) đi qua ba điểm A(1;1;1), B(2;3;-1), C(0;3;-2). Một vectơ pháp tuyến của mặt phẳng (P) là:
Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M(2;6;-3) và vuông góc với hai mặt phẳng (Oxy), (Oyz) là:
Trong không gian Oxyz, cho điểm A di động trên mặt phẳng (P): 2x - y - 2z = 0, điểm B di động trên mặt phẳng (Q): 4x - 2y - 4z - 9 = 0. Khoảng cách giữa hai điểm A và B nhỏ nhất là: