Tích các nghiệm của phương trình là:
A. 1.
B. 2
C.
D. 3.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Điều kiện: x > 0
Ta có:
![]()

Vậy tập nghiệm của phương trình đã cho là
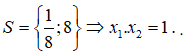
Chọn A
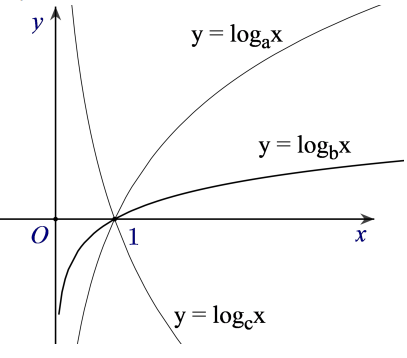
Hình bên là đồ thị của ba hàm số được vẽ trên cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?