Cho khối lăng trụ ABC.A'B'C'. Tỉ số thể tích giữa khối chóp A'.ABC và khối lăng trụ đó là
A.
B.
C.
D.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Chọn B.
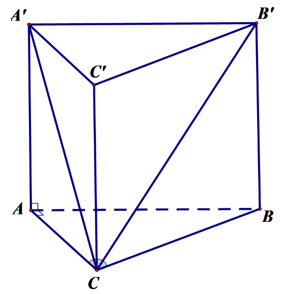
![]()
chính là góc tạo bởi đường chéo BC’ và mặt phẳng (AA’C’C).
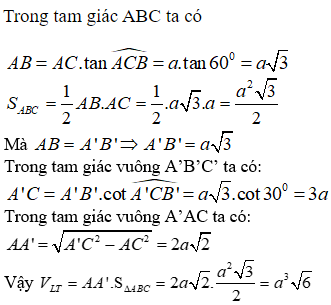
Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Mặt bên (SAB) là tam giác vuông cân tại S và thuộc mặt phẳng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD biết BD = a,
Cho hình chóp S.ABC có SA ⊥ (ABC), đáy ABC là tam giác đều. Tính thể tích khối chóp S.ABC biết AB = a; SA = a.
Cho khối chóp S.ABCD có đáy là hình bình hành. Mặt phẳng (SAC) chia khối chóp S.ABCD thành mấy khối tứ diện.
I. Trắc nghiệm (5 điểm)
Có bao nhiêu phép tịnh tiến biến một đường thẳng thành chính nó?
I. Tự luận ( 5 điểm)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh , cạnh bên SA vuông góc với mặt phẳng đáy; mặt bên (SBC) tạo với mặt đáy (ABC) một góc bằng 45°. Thể tích khối chóp S.ABC theo a bằng?
Cho hình chóp S.ABC. Gọi (α) là mặt phẳng qua C và song song với AB. (α) cắt SA, SB lần lượt tại M, N. Tính tỉ số biết (α) chia khối chóp thành 2 phần có thể tích bằng nhau.
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ trên (ABC) là trung điểm của AB. Mặt phẳng (AA'C'C) tạo với đáy một góc bằng 45°. Tính thể tích V của khối lăng trụ ABC.A'B'C'?