Tính diện tích xung quanh Sxq của hình trụ có đường cao h = a và thể tích V=πa3
A. Sxq=4πa2
B. Sxq=6πa2
C. Sxq=8πa2
D. Sxq=2πa2
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Chọn D.
+ Thể tích hình trụ được tính bằng công thức V = πr2h
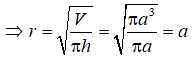
+ Diện tích xung quanh của hình trụ là Sxq = 2πrh = 2πa2.
Một khối trụ có bán kính đáy bằng r có thiết diện qua trục là một hình vuông. Tính diện tích xung quanh của khối trụ đó.
Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6π(cm) và thiết diện đi qua trục là một hình chữ nhật có độ dài đường chéo bằng 10 cm.
Từ một tấm tôn hình chữ nhật kích thước 50cm người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):
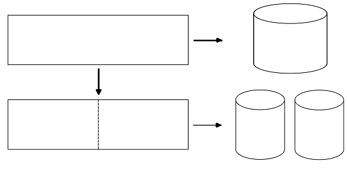
- Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng
- Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu là thể tích của thùng được theo cách 1 và là tổng thể tích của hai thùng được theo cách 2. Tính tỉ số
Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ. Đẳng thức luôn đúng là?
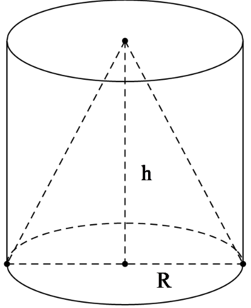
Cho một hình trụ có bán kính đáy R, chiều cao h và thể tích ; một hình nón có đáy trùng với một đáy của hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (hình vẽ bên dưới) và có thể tích . Khẳng định nào sau đây là khẳng định đúng ?
Tính diện tích toàn phần của hình trụ có bán kính đáy a và đường cao
Tính diện tích xung quanh của hình trụ biết hình trụ có bán kính đáy a và đường cao là
Trong không gian, cho hình chữ nhật ABCD có Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần của hình trụ đó.