Cho hình nón đỉnh S, đáy là đường tròn (O; r). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho . Tính theo r khoảng cách từ O đến (SAB).
A.
B.
C.
D.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án B
Phương pháp:
+) Xác định khoảng cách từ O đến (SAB)
+) Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách vừa xác định được.
Cách giải:
Gọi I là trung điểm của AB, kẻ OH vuông góc SI tại H.
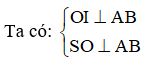
![]()
![]()
![]()
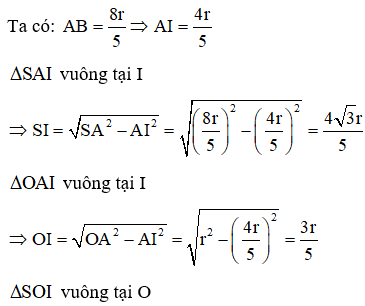
![]()
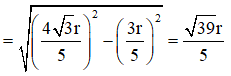
ΔSOI vuông tại O, OH ⊥ SI ⇒ OH.SI = SO.OI
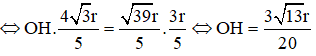
Cho hình chóp S.BACD có đáy ABCD là hình chữ nhật, . Cạnh bên và SA vuông góc với (ABCD). Tính theo a thể tích V của khối chóp S.ABCD
Một hình nón có chiều cao bằng a và thiết diện qua trục của hình nón đó là tam giác vuông. Tính theo a diện tích xung quanh của hình nón đó.
Một xưởng in có 8 máy in, mỗi máy in được 4000 bản in khổ giấy A4 trong một giờ. Chi phí để bảo trì, vận hành một máy mỗi lần in là 50 nghìn đồng. Chi phí in ấn của n máy chạy trong một giờ là 20(3n + 5) nghìn đồng. Hỏi nếu in 50 000 bản in khổ A4 thì phải sử dụng bao nhiêu máy để thu được lãi nhiều nhất?
Cho hình chóp đều S.ABCD có tất cả các cạnh bằng nhau. Khẳng định nào đúng?
Cho hình trụ có bán kính đáy bằng r, chiều cao bằng h. Khẳng định nào sai?
Ông An gửi 100 triệu đồng vào ngân hàng với hình thức lãi kép, kỳ hạn 1 năm với lãi suất 8%/năm. Sau 5 năm ông rút toàn bộ tiền và dùng một nửa để sửa nhà, số tiền còn lại ông tiếp tục gửi vào ngân hàng với kỳ hạn và lãi suất như lần trước. Số tiền lãi mà ông An nhận được sau 10 năm gửi gần nhất với giá trị nào sau đây?
Cho hàm số có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau