Cho các số phức z1=−3i;z2=4+i và z thỏa mãn |z−i|=2. Biểu thức T=|z−z1|+2|z−z2| đạt giá trị nhỏ nhất khi z=a+bi(a,b∈R). Hiệu a - b bằng:
A. 3−6√1317
B. 6√13−317
C. 3+6√1317
D. -3+6√1317
Giải bởi qa.haylamdo.com
Đáp án C
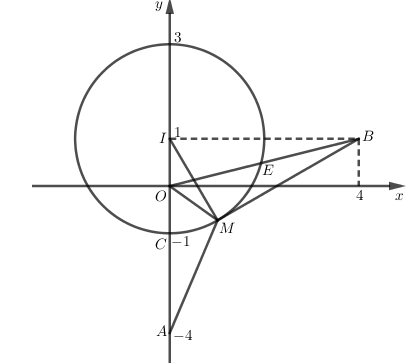
Trên mặt phẳng tọa độ Oxy, gọi A(0;-3) là điểm biểu diễn số phức z1, B(4;1) là điểm biểu diễn số phức z2, I (0;1) là điểm biểu diễn số phức I và M là điểm biểu diễn cho số phức z.
Cho số phức z thỏa mãn |z−1−i|=1, số phức w thỏa mãn |ˉw−2−3i|=2. Tính giá trị nhỏ nhất của |z−w|
Cho hai số phức u, v thỏa mãn 3|u−6i|+3|u−1−3i|=5√10,|v−1+2i|=|ˉv+i|. GTNN của |u−v| là:
Cho các số phức z, w thỏa mãn |z−5+3i|=3,|iw+4+2i|=2. Tìm giá trị lớn nhất của biểu thức T=|3iz+2w|
Xét các số phức z=a+bi(a,b∈R) thỏa mãn điều kiện |z−3−2i|=2. Tính a + b khi |z+1−2i|+2|z−2−5i| đạt giá trị nhỏ nhất.
Cho số phức z thỏa mãn |z|≤2. GTNN của biểu thức P=2|z+1|+2|z−1|+|z−ˉz−4i| bằng:
Trong số các số phức z thỏa mãn điều kiện |z−4+3i|=3, gọi z0 là số phức có mô đun lớn nhất. Khi đó |z0| là:
Cho hai số phức z1=r1(cosφ1+isinφ1),z2=r2(cosφ2+isinφ2). Khi đó:
Trong các số phức z thỏa mãn |z+3+4i|=2, gọi z0 là số phức có mô đun nhỏ nhất. Khi đó:
Cho số phức z=−2+2√3i. Tìm các số nguyên dương n để zn là số thực
Cho số phức z thỏa điều kiện |z+2|=|z+2i|. Giá trị nhỏ nhất của biểu thức P = |z−1−2i|+|z−3−4i|+|z−5−6i| được viết dưới dạng a+b√17√2 với a, b là các hữu tỉ. Giá trị của a + b là:
Cho các số phức w, z thỏa mãn |w+i|=3√55 và 5w=(2+i)(z−4). Giá trị lớn nhất của biểu thức P=|z−1−2i|+|z−5−2i| bằng:
