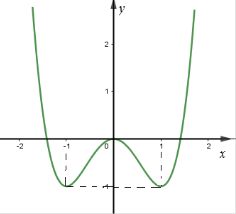
A. 3
B. 1
C. 2
D. 4
Giải bởi qa.haylamdo.com
Đáp án A
Phương pháp:
* Định nghĩa tiệm cận ngang của đồ thị hàm số y=f(x)
Nếu limx→+∞f(x)=a hoặc limx→−∞f(x)=a⇒y=a là TCN của đồ thị hàm số.
* Định nghĩa tiệm cận đứng của đồ thị hàm số y=f(x)
Nếu limx→a+f(x)=−∞ hoặc limx→a−f(x)=+∞ hoặc limx→a−f(x)=−∞ thì x=a là TCĐ của đồ thị hàm số.
Cách giải:
Tập xác định: D=R\{−2;2}
limx→∞=limx→∞2x+14−x2=limx→∞2x+1x24x2−1=0⇒ Đồ thị hàm số có 1 tiệm cận ngang là y=0
limx→−2−2x+14−x2=+∞, limx→−2+2x+14−x2=−∞, limx→2−2x+14−x2=+∞, limx→2+2x+14−x2=−∞
Đồ thị có 2 đường tiệm cận đứng là x= - 2 và x = 2.
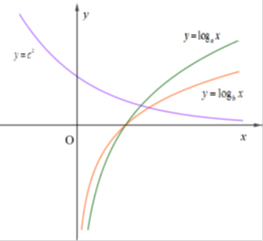
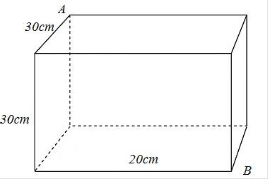
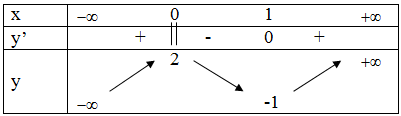
Khẳng định nào sau đây đúng?
