Gọi V1,V2, lần lượt là thể tích của khối tứ diện đều và khối lập phương có chung mặt cầu
ngoại tiếp. Khi đó, bằng
A.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Phương pháp giải:
Bước 1: Lập tỉ lệ giữa cạnh của hình tứ diện đều và bán kính mặt cầu ngoại tiếp, tỉ lệ giữa cạnh hình lập phương và bán kính mặt cầu ngoại tiếp
Bước 2: Lập tỉ số về thể tích giữa tứ diện đều và mặt cầu ngoại tiếp, giữa hình lập phương và mặt cầu ngoại tiếp.
Bước 3: Tính
Giải chi tiết:
Bước 1: Gọi a là độ dài cạnh của tứ diện đều khi đó ta có:
Gọi b là độ dài hình lập phương, ta có:
Bước 2: Tỉ số cạnh của tứ diện đều và lập phương có cùng mặt cầu ngoại tiếp
Bước 3: Tính
Thể tích tứ diện đều cạnh a là
Thể tích khối lập phương cạnh b là :
Vậy tỉ lệ thể tích:
Chọn D.
Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 lập được bao nhiêu số tự nhiên gồm 3 chữ số đôi một khác nhau và số đó chia hết cho 3.
Trong hình vẽ, xe A kéo xe B bằng một sợi dây dài 39m qua một ròng rọc ở độ cao 12m. Xe A xuất phát từ N và chạy với vận tốc không đổi 2 m/s theo chiều mũi tên.
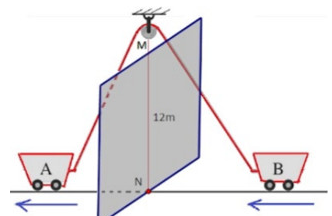
a) Đặt và , (đơn vị mét). Tìm một hệ thức liên hệ giữa x và y .
b) Tính vận tốc của xe B khi xe A cách N một đoạn 5m.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc BAD = 60°. Hình chiếu vuông góc của S lên mặt phẳng đáy là trọng tâm G của tam giác BCD, góc giữa SA và đáy bằng 60°
a) Tính thể tích khối chóp S.ABCD.
b) Tính khoảng cách giữa hai đường thẳng AC và SB.
Một nhà máy sản xuất bóng đèn trang trí với chi phí sản xuất 12 USD mỗi bóng đèn. Nếu giá bán mỗi bóng đèn là 20 USD thì nhà máy dự tính bán được 2000 bóng mỗi tháng. Nếu cứ tăng giá bán mỗi bóng đèn lên 1 USD thì số bóng đèn bán được mỗi tháng giảm đi 100 bóng đèn. Để nhà máy có lợi nhuận lớn nhất, giá bán mỗi bóng đèn là
Một ô tô đang chạy thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc trong đó t (giây) là khoảng thời gian tính từ lúc bắt đầu đạp phanh và a là một hằng số dương. Biết rằng từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển được 36m. Khẳng định nào sau đây đúng?
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Biết với H thuộc cạnh AB thỏa mãn AB=3AH. Góc tạo bởi SA và mặt phẳng (ABC) bằng . Khoảng cách giữa hai đường thẳng SA và BC là
Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho đường thẳng và mặt phẳng . Phương trình đường thẳng d’ đối xứng với d qua (P) là
Một lô hàng có 30 sản phẩm trong đó có 5 phế phẩm. Lấy ngẫu nhiên đồng thời 6 sản phẩm của lô hàng đó. Xác suất để trong 6 sản phẩm lấy ra có không quá 2 phế phẩm là
Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho 4 điểm A(1;5;4), B(-3;1;4),
C(5;4;1), D(-2;1;-3). Bán kính mặt cầu ngoại tiếp tứ diện ABCD bằng
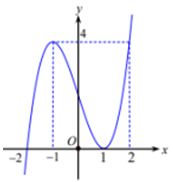
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. Số các giá trị nguyên của m để phương trình có đúng ba nghiệm phân biệt thuộc đoạn là
Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho mặt phẳng , mặt cầu . Gọi là đường thẳng nằm trong mặt phẳng P, đi qua và cắt (S) tại 2 điểm M, N. Độ dài đoạn thẳng MN nhỏ nhất là
Xét các số phức z thỏa mãn . Giá trị nhỏ nhất của biểu thức bằng