Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có phương trình đường phân giác trong góc A là d1:x+y+2=0, phương trình đường cao vẽ từ B là d2:2x−y+1=0, cạnh AB đi qua M(1;−1). Tìm phương trình cạnh AC.
A.x+2y−7=0
B.5x+2y+7=0
C.x+2y+7=0
D.2x+5y+7=0
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
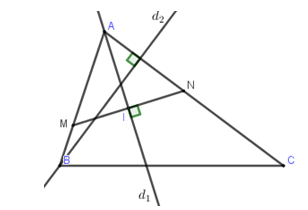
Gọi N là điểm đối xứng của M qua \[{d_1} \Rightarrow N \in AC\]
\[\overrightarrow {MN} = ({x_N} - 1,\,\,{y_N} + 1)\]
Ta có: \[\overrightarrow {MN} \]cùng phương\[{\vec n_{{d_1}}} = (1;\,\,1)\]
\[ \Leftrightarrow \,\,1({x_N} - 1) - 1({y_N} + 1) = 0 \Leftrightarrow {x_N} - {y_N} = 2\,\,\,(1)\]
Tọa độ trung điểm I của\[MN:{x_I} = \frac{1}{2}\left( {1 + {x_N}} \right),{y_I} = \frac{1}{2}\left( { - 1 + {y_N}} \right)\]
\[I \in \left( {{d_1}} \right) \Leftrightarrow \frac{1}{2}\left( {1 + {x_N}} \right) + \frac{1}{2}\left( { - 1 + {y_N}} \right) + 2 = 0 \Leftrightarrow {x_N} + {y_N} + 4 = 0\,\,\,\,(2)\]
Giải hệ (1) và (2) ta được \[N\left( { - 1; - 3} \right)\]
Phương trình cạnh AC vuông góc với \[{d_2}\] có dạng: \[x + 2y + C = 0.\]
\[N \in AC \Leftrightarrow - 1 + 2.( - 3) + C = 0 \Leftrightarrow C = 7\]
Vậy, phương trình cạnh \[AC:x + 2y + 7 = 0.\]
Đáp án cần chọn là: CCâu 21. Xét trong mặt phẳng tọa độ Oxy, cặp điểm nào dưới đây nằm cùng phía so với đường thẳng \[x - 2y + 3 = 0?\]
A.M(0;1) và P(0;2).
B.P(0;2) và N(1;1).
C.M(0;1) và Q(2;−1).
D.M(0;1) và N(1;5).
Ta thế tọa độ M(0;1) và P(0;2) vào đường thẳng:
\[\left( {0 - 2.1 + 3} \right)\left( {0 - 2.2 + 3} \right) < 0\] nên loại A.
Ta thế tọa độ N(1;1) và P(0;2) vào đường thẳng:
\[\left( {1 - 2.1 + 3} \right)\left( {0 - 2.2 + 3} \right) < 0\] nên loại B.
Ta thế tọa độ M(0;1) và Q(2;−1) vào đường thẳng:
\[\left( {0 - 2.1 + 3} \right)\left( {2 - 2.\left( { - 1} \right) + 3} \right) >0\] nên chọn C.
Đáp án cần chọn là: C
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng \[(d):3x - 4y - 12 = 0\]Phương trình đường thẳng \[\left( \Delta \right)\;\]đi qua M(2;−1) và tạo với (d) một góc \[{45^o}\] có dạng \[ax + by + 5 = 0\], trong đó a,b cùng dấu. Khẳng định nào sau đây đúng?
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng đi qua hai điểm A(1;2), B(4;6), tìm tọa độ điểm M trên trục Oy sao cho diện tích \[\Delta MAB\] bằng 1.
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(1;2), B(0;3) và C(4;0). Chiều cao của tam giác kẻ từ đỉnh A bằng:
Trong mặt phẳng với hệ toạ độ Oxy, cho 4 điểm A(1;0),B(−2;4),C(−1;4),D(3;5). Tìm toạ độ điểm M thuộc đường thẳng \[\left( \Delta \right):3x - y - 5 = 0\;\]sao cho hai tam giác MAB,MCD có diện tích bằng nhau.
Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M(x0;y0) và đường thẳng \[\Delta :ax + by + c = 0\]. Khoảng cách từ điểm M đến \[\Delta \] được tính bằng công thức:
Tìm tất cả các giá trị của tham số m để khoảng cách từ điểm A(−1;2) đến đường thẳng \[\Delta :mx + y - m + 4 = 0\;\] bằng \[2\sqrt 5 \].
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(3;−4), B(1;5) và C(3;1). Tính diện tích tam giác ABC.
Trên mặt phẳng tọa độOxy, cho tam giác ABC có tọa độ các đỉnh là A(2;3),B(5;0) và C(−1;0). Tìm tọa độ điểm M thuộc cạnh BC sao cho diện tích tam giác MAB bằng hai lần diện tích tam giác MAC
Trong mặt phẳng Oxy cho điểm A(−1;2);B(3;4) và đường thẳng \[{\rm{\Delta }}:\,\,x - 2y - 2 = 0\]. Tìm điểm \[M \in \Delta \] sao cho \[2A{M^2} + M{B^2}\] có giá trị nhỏ nhất.
Cho hai đường thẳng \[{d_1}:3x + 4y + 12 = 0\] và \[{d_2}:\left\{ {\begin{array}{*{20}{c}}{x = 2 + at}\\{y = 1 - 2t}\end{array}} \right.\]. Tìm các giá trị của tham số a để d1 và d2 hợp với nhau một góc bằng 450.
Khoảng cách từ giao điểm của hai đường thẳng \[x - 3y + 4 = 0\] và \[2x + 3y - 1 = 0\;\]đến đường thẳng \[\Delta :3x + y + 4 = 0\;\] bằng:
Cho đường thẳng \[{d_1}:x + 2y - 7 = 0\] và \[{d_2}:2x - 4y + 9 = 0\]. Tính cosin của góc tạo bởi giữa hai đường thẳng đã cho.
Lập phương trình đường thẳng (Δ) đi qua M(2;7) và cách N(1;2) một khoảng bằng 1.
Trong mặt phẳng với hệ tọa độ Oxy, cho \[\Delta ABC\] cân có đáy là BC.BC. Đỉnh A có tọa độ là các số dương, hai điểm B và C nằm trên trục Ox, phương trình cạnh AB: \[y = 3\sqrt 7 (x - 1)\] Biết chu vi của \[\Delta ABC\] bằng 18, tìm tọa độ các đỉnh A,B,C.
Lập phương trình đường phân giác trong của góc A của ΔABC biết A(2;0);B(4;1);C(1;2)