Cho tam giác ABC, vuông tại A (AB < AC). Vẽ đường cao AH (H Î BC). Lấy điểm D sao cho H là trung điểm BD.

a) Chứng minh ∆ABC $\backsim$  ∆HBA;

b) Qua C dựng đường thẳng vuông góc với tia AD, cắt AD tại E. Chứng minh AH.CD = CE.AD;

c) Chứng minh ∆HDE $\backsim$  ∆ADC và BD.AC = 2AD.HE;

d) AH cắt CE tại F. Chứng minh AF² = 2BF.AE.

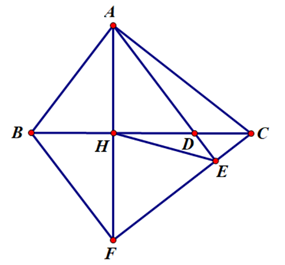
a) Xét ∆ABC và ∆HBA có:

$\widehat{BAC}=\widehat{BHA}={90}^o$(gt)

$\widehat{ABC}$ chung (gt)

Do đó ∆ABC $\backsim$  ∆HBA (g.g);

b) Xét ∆ADH và ∆CDE có:

$\widehat{AHD}=\widehat{CED}$= 90^o (gt)

$\widehat{ADH}=\widehat{CDE}$ (hai góc đối đỉnh)

Do đó ∆ADH $\backsim$  ∆CDE (g.g).

Suy ra $\frac{AH}{CE}=\frac{AD}{CD}$  (các cạnh tương ứng tỉ lệ)

Vậy: AH.CD = CE.AD (đccm)

c) Ta có: ∆ADH $\backsim$  ∆CDE (câu b)

Suy ra  $\frac{DH}{DE}=\frac{DA}{DC}$ (các cạnh tương ứng tỉ lệ)

Xét ∆HDE và ∆ADC có:

$\frac{DH}{DE}=\frac{DA}{DC}$ (cmt)

$\widehat{HDE}=\widehat{ADC}$ (hai góc đối đỉnh)

Suy ra ∆HDE $\backsim$  ∆ADC (c.g.c)

Suy ra $\frac{HD}{HE}=\frac{AD}{AC}$  (các cạnh tương ứng tỉ lệ)

Do đó HD.AC = AD.HE

Mặc khác H là trung điểm của BD (gt) $\Rightarrow HD=\frac{BD}{2}$ ;

Suy ra: HD.AC = $\frac{BD}{2}$ .AC = AD.HE

Vậy BD.AC = 2AD.HE.

d) Vì AH vừa là đường cao vừa là trung tuyến của BD nên AH là trung trực của BD.

Suy ra ∆ADB cân tại A và AH là phân giác của $\widehat{BAD}$  hay $\widehat{BAH}=\widehat{HAD}$ .

Từ câu a: ∆ABC $\backsim$  ∆HBA suy ra $\widehat{BAH}=\widehat{BCA}$  (hai góc tương ứng);

Từ câu b: ∆ADH $\backsim$  ∆CDE suy ra $\widehat{HAD}=\widehat{ECD}$  (hai góc tương ứng).

Do đó $\widehat{ACH}=\widehat{HCF}$  hay CH là phân giác của $\widehat{ACF}$ .

Mặc khác HC vừa là đường cao của ∆ACF nên HC là trung trực của AF.

Hay BC là đường trung trực của đoạn thẳng AF.

Do đó BA = BF.

Suy ra ∆ABF cân tại B có $\widehat{BAH}=\widehat{BFH}$ .

Xét ∆BHF và ∆FEA có:

$\widehat{BFH}=\widehat{FAE}=\widehat{BAH}$ (cmt)

$\widehat{BHF}=\widehat{FEA}$= 90^o (gt)

Suy ra ∆BHF $\backsim$  ∆FEA (g.g)

Suy ra $\frac{BF}{HF}=\frac{FA}{EA}=\frac{AF}{AE}$  (các cạnh tương ứng tỉ lệ).

Do đó BF.AE = HF.AF.

Vì H là trung trực AF nên $HF=\frac{AF}{2}$ .

Suy ra $BF.AE=\frac{AF}{2}.AF$

Do đó AF² = 2BF.AE (đpcm).