Đề kiểm tra giữa kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề số 13
-
1646 lượt thi
-
5 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Giải phương trình:
a) 7 + 2x = 32 – 3x;
b) x+45−x+4=x3−x−22 ;
c) x2 + (x + 3)(x – 5) = 9;
d) x+2x−2−3x+2+3x+104−x2=0 .
a) 7 + 2x = 32 – 3x
Û 2x + 3x = 32 – 7
Û 5x = 25
Û x = 5
Vậy tập nghiệm của phương trình là S = {5};b) x+45−x+4=x3−x−22
⇔6(x+4)30−30x30+4.3030=10.x30−15(x−2)30⇔6x+2430−30x30+12030=10x30−15x−3030⇔6x+24−30x+12030=10x−15x+3030
Û 6x + 24 – 30x + 120 = 10x – 15x + 30
Û –24x + 144 = –5x + 30
Û 24x – 5x = 144 – 30
Û 19x = 114
Û x = 6
Vậy tập nghiệm của phương trình là S = {6};
c) x2 + (x + 3)(x – 5) = 9
Û x2 – 9 + (x + 3)(x – 5) = 0
Û (x – 3)(x + 3) + (x + 3)(x – 5) = 0
Û (x + 3) [(x – 3) + (x – 5)] = 0
Û (x + 3) (x – 3 + x – 5) = 0
Û (x + 3) (2x – 8) = 0
⇔[x
Vậy tập nghiệm của phương trình là S = {– 3; 4};
d)
Điều kiện xác định:
Ta có:
Þ (x + 2)2 – (3x – 6) – (3x + 10) = 0
Û (x + 2)2 – 3x + 6 – 3x – 10 = 0
Û (x + 2)2 – 6x – 4 = 0
Û x2 + 4x + 4 – 6x – 4 =0
Û x2 – 2x = 0
Û x.(x – 2) = 0
Vậy tập nghiệm của phương trình là S = {0}.
Câu 2:
Gọi x (km) là chiều dài quãng đường AB lúc đi (x > 0).
Chiều dài quãng đường tắt từ B về A ngắn hơn đường lúc đi 5 km là x – 5 (km).
Vận tốc lúc đi về từ B đến A nhỏ hơn vận tốc lúc đi là: 12 – 2 = 10 (km/h).
Thời gian người đi xe đạp đi hết quãng đường từ A đến B là:
tAB = (h).
Thời gian người đi xe đạp đi hết quãng đường tắt từ B về A là:
tBA = (h).
Đổi 40 phút = giờ.
Vì thời gian lúc đi từ A đến B ít hơn thời gian lúc đi từ B về A là 40 phút nên ta có phương trình:
Û 6x – 30 – 5x = 40
Û 6x – 5x = 40 + 30
Û x = 70 (thoản mãn)
Vậy chiều dài quãng đường AB lúc đi là 70 km.Câu 3:
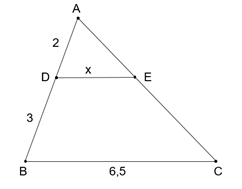
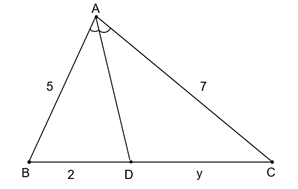
a) Theo hình vẽ ta có: AB = AD + DB = 2 + 3 = 5.
Áp dụng hệ quả định lý Ta – let trong ∆ABC có DE // BC, D Î AB, E Î AC ta có:
.
Vậy x = 2,6.b) Trong ∆ABC có AD là tia phân giác góc , D Î BC ta có:
Vậy y = 2,8.
Câu 4:
Cho tam giác ABC, vuông tại A (AB < AC). Vẽ đường cao AH (H Î BC). Lấy điểm D sao cho H là trung điểm BD.
a) Chứng minh ∆ABC ∆HBA;
b) Qua C dựng đường thẳng vuông góc với tia AD, cắt AD tại E. Chứng minh AH.CD = CE.AD;
c) Chứng minh ∆HDE ∆ADC và BD.AC = 2AD.HE;
d) AH cắt CE tại F. Chứng minh AF2 = 2BF.AE.
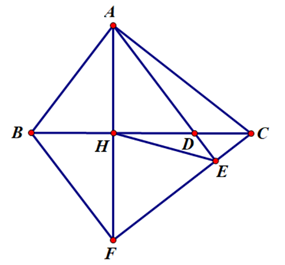
a) Xét ∆ABC và ∆HBA có:
(gt)
chung (gt)
Do đó ∆ABC ∆HBA (g.g);b) Xét ∆ADH và ∆CDE có:
= 90o (gt)
(hai góc đối đỉnh)
Do đó ∆ADH ∆CDE (g.g).
Suy ra (các cạnh tương ứng tỉ lệ)
Vậy: AH.CD = CE.AD (đccm)c) Ta có: ∆ADH ∆CDE (câu b)
Suy ra (các cạnh tương ứng tỉ lệ)
Xét ∆HDE và ∆ADC có:
(cmt)
(hai góc đối đỉnh)
Suy ra ∆HDE ∆ADC (c.g.c)
Suy ra (các cạnh tương ứng tỉ lệ)
Do đó HD.AC = AD.HE
Mặc khác H là trung điểm của BD (gt) ;
Suy ra: HD.AC = .AC = AD.HE
Vậy BD.AC = 2AD.HE.d) Vì AH vừa là đường cao vừa là trung tuyến của BD nên AH là trung trực của BD.
Suy ra ∆ADB cân tại A và AH là phân giác của hay .
Từ câu a: ∆ABC ∆HBA suy ra (hai góc tương ứng);
Từ câu b: ∆ADH ∆CDE suy ra (hai góc tương ứng).
Do đó hay CH là phân giác của .
Mặc khác HC vừa là đường cao của ∆ACF nên HC là trung trực của AF.
Hay BC là đường trung trực của đoạn thẳng AF.
Do đó BA = BF.
Suy ra ∆ABF cân tại B có .
Xét ∆BHF và ∆FEA có:
(cmt)
= 90o (gt)
Suy ra ∆BHF ∆FEA (g.g)
Suy ra (các cạnh tương ứng tỉ lệ).
Do đó BF.AE = HF.AF.
Vì H là trung trực AF nên .
Suy ra
Do đó AF2 = 2BF.AE (đpcm).
Câu 5:
Cho x = by + cz (1); y = ax + cz (2); z = ax + by (3) và x + y + z ≠ 0; xyz ≠ 0.
Chứng minh đẳng thức .x = by + cz (1); y = ax + cz (2); z = ax + by (3) và x +y + z ≠ 0; xyz ≠ 0.
Lấy (1) trừ (2), ta được:
x – y = (by + cz) − (ax + cz)
Û x – y = by – ax + cz – cz
Û x – y = by – ax
Û x + ax = by + y
Û x(a + 1) = y(b + 1) (*)Lấy (2) trừ (3), ta được:
y – z = (ax + cz) − (ax + by)
Û y – z = ax – ax + cz – by
Û y – z = cz – by
Û y + by = z + cz
Û y(b + 1) = z (c + 1) (**)Lấy (1) trừ (3), ta được:
x – z = (by + cz) − (ax + by)
Û x – z by – by + cz – ax
Û x – z = cz – ax
Û x + ax = cz + z
Û x(1 + a) = z(c + 1) (***)Đặt x(a + 1) = y(b + 1) = z(c + 1) = t
(do x, y, z ≠ 0)
Thay vào biểu thức , ta được:
Với x = by + cz (1); y = ax + cz (2); z = ax + by (3)
t = x(a+1) = ax + x = ax + by + cz
Vậy .
