Cho tam giác ABC có , từ trung điểm M của AB kẻ tia Mx song song BC, từ C kẻ tia Cy song song AB sao cho Mx cắt Cy tại N.
Chứng minh .
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Phương pháp:
Sử dụng dấu hiệu nhận biết và tính chất của hình bình hành, dấu hiệu nhận biết tam giác vuông, chứng minh tam giác bằng nhau và tính chất trọng tâm của tam giác.
Cách giải:
Vì BMNC là hình bình hành (cmt) nên .
Lại có: .
Tam giác có đường trung tuyến NM bằng nửa cạnh đối AB nên tam giác ABN vuông tại N, hay AN vuông góc với BN (đpcm).
Cho các số x, y, z dương thỏa mãn .
Tìm giá trị nhỏ nhất của biểu thức .
Cho biểu thức với .
Cho tam giác ABC có , từ trung điểm M của AB kẻ tia Mx song song BC, từ C kẻ tia Cy song song AB sao cho Mx cắt Cy tại N.
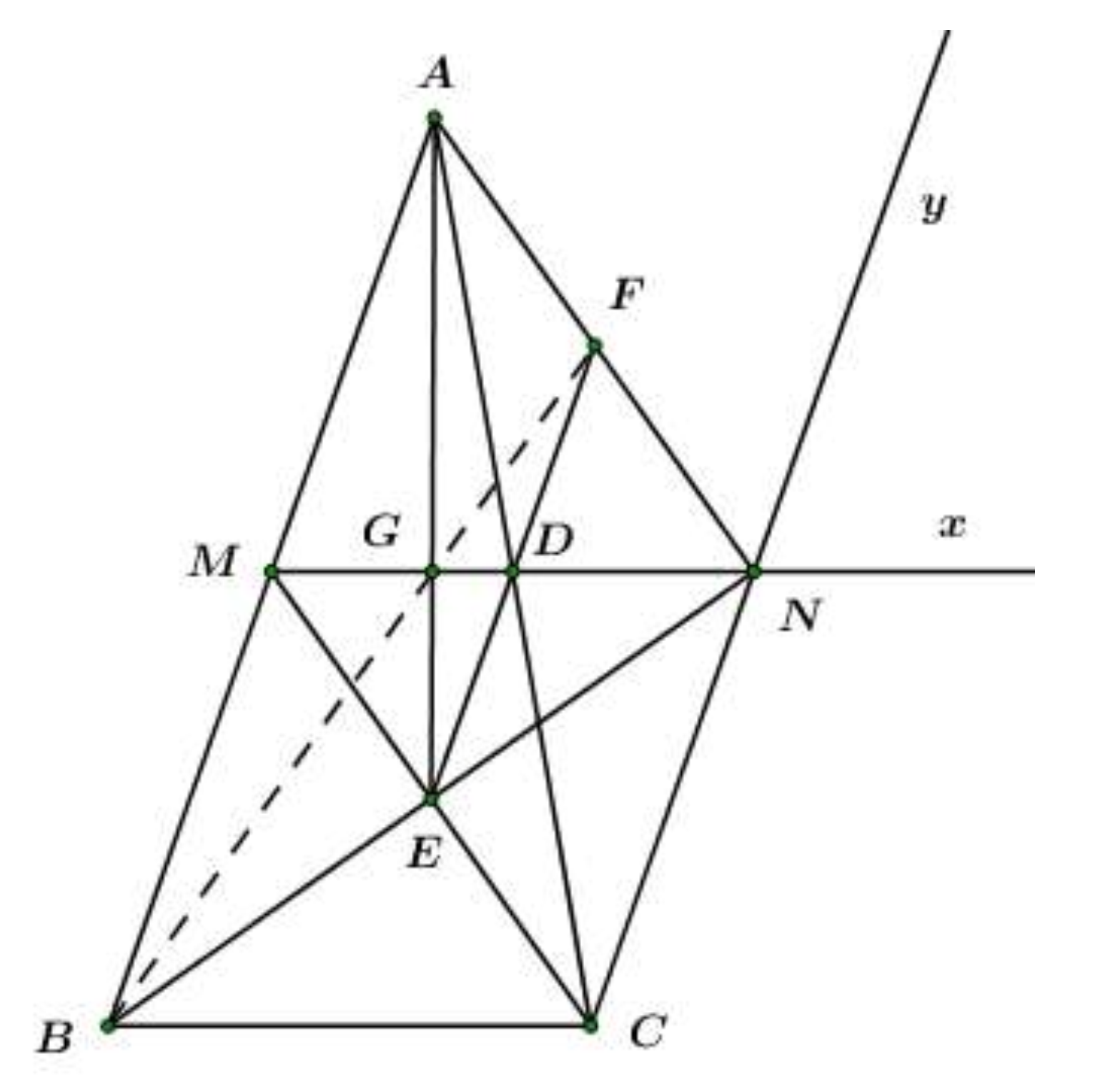
Gọi D là giao điểm của MN với AC, E là giao điểm của MC với BN, F là giao điểm của ED với AN. Chứng minh .
Cho tam giác ABC có , từ trung điểm M của AB kẻ tia Mx song song BC, từ C kẻ tia Cy song song AB sao cho Mx cắt Cy tại N.
Gọi G là giao điểm của AE với MN. Chứng minh B, G, F thẳng hàng.
Cho biểu thức với .
Tính giá trị của biểu thức P, với x thỏa mãn .
Cho tam giác ABC có , từ trung điểm M của AB kẻ tia Mx song song BC, từ C kẻ tia Cy song song AB sao cho Mx cắt Cy tại N.
Chứng minh tứ giác MBCN là hình bình hành.