Cho tam giác ABC vuông tại A có AH là đường cao (H thuộc BC), N là trung điểm của AB. Biết AB=6cm, AC=8cm. Gọi E là hình chiếu vuông góc của H lên AC và T là điểm đối xứng của N qua I với I là giao điểm của CN và HE. Chứng minh tứ giác NETH là hình bình hành.
Giải bởi qa.haylamdo.com
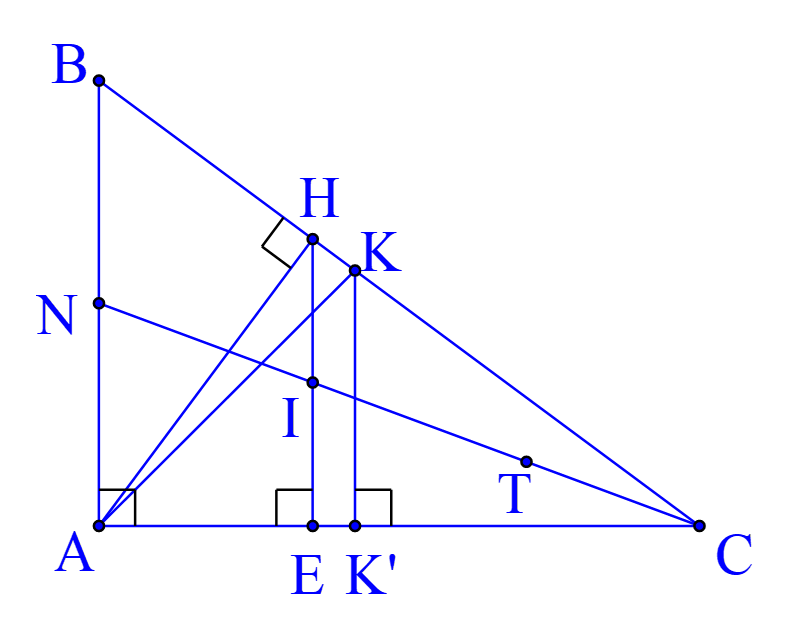
Ta chứng minh I là trung điểm của HE.
Vì HEAC nên HE // BA. Theo định lí Talet ta có: .
Vì NA = NB nên IE = IH. Do đó I là trung điểm của HE.
Theo giả thiết thì I là trung điểm của NT.
Tứ giác NETH có hai đường chéo NT và EH có chung trung điểm I nên NETH là hình bình hành.
Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia HC lấy điểm D sao cho HD = AH. Đường thẳng vuông góc với BC tại D cắt AC tại E. Gọi M là trung điểm của BE, tia AM cắt BC tại G. Chứng minh: .
Cho tam giác ABC vuông tại A có AH là đường cao (H thuộc BC), N là trung điểm của AB. Biết AB=6cm, AC=8cm.Vẽ AK là tia phân giác của góc (K thuộc BC). Tính AK?
Cho tam giác ABC có I là giao điểm của ba đường phân giác. Đường thẳng qua I cắt các đường thẳng lần lượt tại sao cho nằm cùng phía đối với điểm I. Chứng minh rằng:
Cho tam giác ABC vuông tại A có G là trọng tâm, BM là đường phân giác. Biết rằng . Chứng minh rằng BM vuông góc với trung tuyến AD.
