Cho tam giác nhọn ABC. Lấy M bất kì trên cạnh BC. Gọi E, F lần lượt là các điểm đối xứng vói M qua AB và AC. Gọi I, K là giao điểm của EF với AB và AC.
a) Chứng minh rằng MA là tia phân giác của .
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
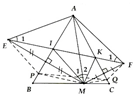
a) Sử dụng tính chất đối xứng trục kết hợp với chứng minh tam giác bằng nhau ta có được và , mà (Tính chất tam giác cân)
=> ĐPCM.
Cho tam giác ABC có AB < AC, gọi d là đường trung trực của BC. Vẽ K đối xứng với A qua d.
a) Tìm đoạn thẳng đối xứng với đoạn thẳng AB qua đường thẳng d; tìm đoạn thẳng đối xứng với đoạn thẳng AC qua đường thẳng d.
b) Khi M cố định, tìm vị trí điểm P AB và Q AC để chu vi tam giác MPQ đạt giá trị nhỏ nhất.
Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C. Chứng minh AC + CB < AM + MB.
Cho tam giác ABC, có = 60°, trực tâm H. Gọi M là điểm đối xứng với H qua BC.
a) Chứng minh BHC = BMC