Cho tứ giác ABCD và một điểm M nằm giữa A và B. Chứng minh rằng MC + MD nhỏ hơn số lớn nhất trong hai tổng AC + AD; BC + BD.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Trước hết ta chứng minh bài toán phụ:
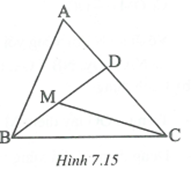
Cho tam giác ABC, điểm M ở trong tam giác (hoặc ở trên một cạnh nhưng không trùng với các đỉnh của tam giác). Chứng minh rằng (h.7.15).
Thật vậy, xét , ta có hay . (1)
Xét có MC < DC + MD. (2)
Cộng từng vế của (1) và (2) ta được:
Bất đẳng thức trên vẫn đúng nếu điểm M nằm trên một cạnh nhưng không trùng với đỉnh của tam giác.
Bây giờ ta vận dụng kết quả trên để giải bài toán đã cho.
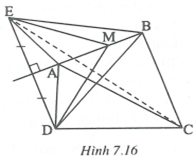
Vẽ điểm E đối xứng với D qua đường thẳng AB (h.7.16).
Khi đó AE = AD; ME = MD và BE = BD.
Vì điểm M nằm giữa A và B nên hoặc điểm M nằm trong hoặc điểm M nằm trong hoặc điểm M nằm trên cạnh EC.
Ta có hay .
Do đó .
Cho tam giác nhọn ABC. Gọi D, E, F lần lượt là các điểm nằm trên các cạnh BC, CA, AB. Xác định vị trí của D, E, F để chu vi tam giác DEF nhỏ nhất.
Cho tam giác ABC. Vẽ điểm D đối xứng với A qua điểm B. Vẽ điểm E đối xứng với B qua C. Vẽ điểm F đối xứng với C qua A. Chứng minh rằng tam giác ABC và tam giác DEF có cùng một trọng tâm.
Cho tam giác ABC, đường phân giác AD và một điểm M ở trong tam giác. Vẽ các điểm N, P, A' đối xứng với M lần lượt qua AB, AC và AD.
a) Chứng minh rằng N và P đối xứng qua AA';
Cho tam giác ABD. Vẽ điểm C đối xứng với A qua BD. Vẽ các đường phân giác ngoài tại các đỉnh A, B, C, D của tứ giác ABCD chúng cắt nhau tạo thành tứ giác EFGH.
a) Xác định dạng của tứ giác EFGH;
Cho tam giác nhọn ABC. Gọi D là điểm nằm giữa B và C. Vẽ các điểm M và N đối xứng với D lần lượt qua AB và AC.
a) Chứng minh rằng góc MAN luôn có số đo không đổi;
Cho góc xOy khác góc bẹt và một điểm G ở trong góc đó. Dựng điểm , điểm sao cho G là trọng tâm của tam giác OAB.
Dựng hình bình hành ABCD biết vị trí trung điểm M của AB, trung điểm N của BC và trung điểm P của CD.
b) Gọi B', C' là các điểm đối xứng với M lần lượt qua các đường phân giác của góc B, góc C. Chứng minh rằng ba đường thẳng AA', BB', CC' đồng quy.
Cho tam giác ABC và O là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là trung điểm của BC, CA, AB. Gọi A', B', C' lần lượt là các điểm đối xứng với O qua D, E, F. Chứng minh rằng ba đường thẳng AA', BB', CC' đồng quy.