Dựng hình bình hành ABCD biết vị trí trung điểm M của AB, trung điểm N của BC và trung điểm P của CD.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
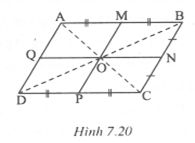
- Phân tích
Giả sử đã dựng được hình bình hành ABCD thỏa mãn đề bài.
Gọi O là giao điểm của hai đường chéo. Ta có M và P đối xứng qua O.
Gọi Q là giao điểm của NO với AD thì Q và N đối xứng qua O.
Vậy điểm Q xác định được, từ đó xác định được hình bình hành ABCD.
- Cách dựng
+ Dựng trung điểm O của MP;
+ Dựng điểm Q đối xứng với N qua O;
+ Qua M và P dựng những đường thẳng song song với NQ; qua N và Q dựng những đường thẳng song song với MP ta được các giao điểm A, B, C, D.
Khi đó tứ giác ABCD là hình bình hành phải dựng.
Các phần còn lại, bạn đọc tự giải.
Cho tứ giác ABCD và một điểm M nằm giữa A và B. Chứng minh rằng MC + MD nhỏ hơn số lớn nhất trong hai tổng AC + AD; BC + BD.
Cho tam giác nhọn ABC. Gọi D, E, F lần lượt là các điểm nằm trên các cạnh BC, CA, AB. Xác định vị trí của D, E, F để chu vi tam giác DEF nhỏ nhất.
Cho tam giác ABC. Vẽ điểm D đối xứng với A qua điểm B. Vẽ điểm E đối xứng với B qua C. Vẽ điểm F đối xứng với C qua A. Chứng minh rằng tam giác ABC và tam giác DEF có cùng một trọng tâm.
Cho tam giác ABC, đường phân giác AD và một điểm M ở trong tam giác. Vẽ các điểm N, P, A' đối xứng với M lần lượt qua AB, AC và AD.
a) Chứng minh rằng N và P đối xứng qua AA';
Cho tam giác ABD. Vẽ điểm C đối xứng với A qua BD. Vẽ các đường phân giác ngoài tại các đỉnh A, B, C, D của tứ giác ABCD chúng cắt nhau tạo thành tứ giác EFGH.
a) Xác định dạng của tứ giác EFGH;
Cho tam giác nhọn ABC. Gọi D là điểm nằm giữa B và C. Vẽ các điểm M và N đối xứng với D lần lượt qua AB và AC.
a) Chứng minh rằng góc MAN luôn có số đo không đổi;
Cho góc xOy khác góc bẹt và một điểm G ở trong góc đó. Dựng điểm , điểm sao cho G là trọng tâm của tam giác OAB.
b) Gọi B', C' là các điểm đối xứng với M lần lượt qua các đường phân giác của góc B, góc C. Chứng minh rằng ba đường thẳng AA', BB', CC' đồng quy.
Cho tam giác ABC và O là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là trung điểm của BC, CA, AB. Gọi A', B', C' lần lượt là các điểm đối xứng với O qua D, E, F. Chứng minh rằng ba đường thẳng AA', BB', CC' đồng quy.