Cho tam giác ABC vuông tại A, điểm D thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB, gọi F là điểm đối xứng với D qua AC. Chứng minh rằng các điểm E và F đối xứng nhau qua điểm A.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
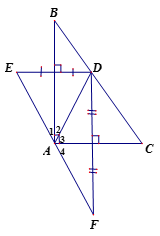
Ta có E đối xứng với D qua AB
=> AB là đường trung trực của ED
=> △AE= AD (1)
=> ADE cân tại A
=> AB là đường phân giác
=> ^A1=^A2 (2)
Ta có F đối xứng với D qua AC
=> AC là đường trung trực của FD
=> AF= AD (3)
=> △ADF cân tại A
=> AC là đường phân giác
=> ^A3=^A4 (4)
Từ (1) và (3) => AE= AF (5)
Ta có ^EAF=^A1+^A2+^A3+^A4 (6)
Từ (2)(4) và (6) suy ra
^EAF=^A2+^A2+^A3+^A3 =2(^A2+^A3) =2^BAC =2.900 =1800
=> E, A, E thẳng hàng (7)
Từ (5) và (7) suy ra E đối xứng với F qua A
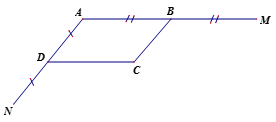
Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Gọi O là điểm bất kỳ nằm trong tam giác ABC. Vẽ M đối xứng với O qua D, vẽ N đối xứng với O qua E. Chứng minh rằng MNCB là hình bình hành.
Cho △ABC có H là trực tâm. Gọi M là trung điểm của BC, K là điểm đối xứng với H qua M. Tính số đo ^ABK; ^ACK
Cho hình thang ABCD (AD//BC). Gọi M, N lần lượt là trung điểm của các cạnh AB, CD; E là một điểm bất kỳ trên cạnh đáy AD và I, K là điểm đối xứng với E lần lượt qua M và N. Chứng minh rằng độ dài IK không phụ thuộc vào vị trí của điểm E
Cho hình vẽ trong đó ABCD là hình bình hành. Chứng minh rằng điểm M đối xứng với điểm N qua C.
Cho ^xOy, điểm A nằm trong góc đó, Vẽ điểm B đối xứng với A qua Ox, C đối xứng với A qua Oy.
a) Chứng minh rằng OB = OC
Cho tam giác ABC, các đường trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng với C qua N. Chứng minh rằng điểm D đối xứng với điểm E qua điểm A.