Cho góc xOy có số đo bằng . Điểm A cố định trên tia Ox sao cho . Lấy điểm B bất kì trên tia Oy. Gọi G là trọng tâm của tam giác OAB. Hỏi khi điểm B di động trên tia Oy thì điểm G di động trên đường nào?
Giải bởi qa.haylamdo.com
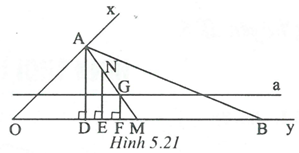
Gọi M là trung điểm của OB.
Khi đó và AG = 2GM.
Gọi N là trung điểm của AG, ta được AN = NG = GM.
Vẽ AD, NE, GF cùng vuông góc với Oy.
Ba đường thẳng AD, NE và GF là ba đường thẳng song song cách đều nên DE = EF = FM
Ta đặt FG = x thì EN = 2x và . Do đó .
Xét vuông cân tại .
Do đó
Điểm G cách Oy một khoảng không đổi là 1cm nên điểm G di động trên đường thẳng a // Oy và cách Oy là 1cm.
Cho tam giác đều ABC cạnh a. Trên các cạnh AB, AC lần lượt lấy các điểm D và E sao cho AD = CE. Tìm giá trị nhỏ nhất của độ dài DE.
Cho góc xOy có số đo bằng . Điểm A cố định trên tia Ox sao cho OA = 2cm. Lấy điểm B bất kì trên tia Oy. Trên tia đối của tia BA lấy điểm C sao cho BC = 2BBA. Hỏi khi điểm B di động trên tia Oy thì điểm C di động trên đường nào?
Cho hình chữ nhật ABCD, đường chéo AC = d. Trên các cạnh AB, BC, CD và DA lần lượt lấy các điểm M, N, P, Q. Tính giá trị nhỏ nhất của tổng:
Cho tam giác ABC vuông tại A. Trên cạnh huyền BC lấy một điểm M. Vẽ và . Tính số đo của góc DHE.
Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AD. Vẽ . Gọi M và N lần lượt là trung điểm của HB và HC.
a) Chứng minh rằng: EM // FN // AD
b) Tam giác ABC phải có thêm điều kiện gì thì ba đường thẳng EM, FN, AD là ba đường thẳng song song cách đều.
