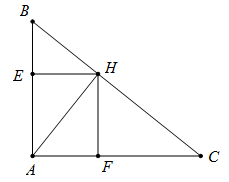
Vẽ tam giác ABC vuông tại A có AB = 4cm; AC = 5cm và AH là đường cao.

a) Tính độ dài đoạn thẳng AH.                           

b) Tính các tỉ số lượng giác: tanB, sinC.

c) Gọi E là hình chiếu của H trên AB và F là hình chiếu của H trên AC.

    Chứng minh AE.AB = AF.AC

Cho nửa đường tròn tâm O có đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc nửa đường tròn (M khác A và B). Đường thẳng qua M vuông góc với OM cắt Ax tại C và cắt By tại D.

a) Chứng minh CA = CM.                                   

b) Chứng minh $\widehat{\text{MOB}}\text{ = 2.}\widehat{\text{ MAO}}$, từ đó suy ra AM song song với OD.     

c) Gọi N là giao điểm của AD và BC. Chứng minh đường thẳng MN vuông góc với đường thẳng AB.

Thực hiện tính:

$A=\sqrt{60}:\sqrt{15}$

Với giá trị nào của x thì $\sqrt{6+x}$ xác định?

Thực hiện tính:

$\frac{1}{\sqrt{2}+\sqrt{3}}+\sqrt{2}$