10 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 17 - Đề 2

Bài tập theo tuần Toán 9 - Tuần 17

Bài tập theo tuần Toán 9 - Tuần 17 - Đề 2

448 lượt thi
10 câu hỏi
30 phút

Danh sách câu hỏi

Câu 1:

Với giá trị nào của x thì $\sqrt{6 + x}$ xác định?

\sqrt{6 + x}

xác định khi 6 + x ≥ 0

Þ x ≥ -6

Câu 2:

Thực hiện tính:

$A = \sqrt{60} : \sqrt{15}$

Xem đáp án

$A = \sqrt{60} : \sqrt{15} = \sqrt{60 : 15}$ (hoặc $= \sqrt{4}$ )

$\sqrt{4} = 2$

Câu 3:

Thực hiện tính:

B = \sqrt{{(2 - \sqrt{5})}^{2}} + \sqrt{4}

Xem đáp án

$B = \sqrt{{(2 - \sqrt{5})}^{2}} + \sqrt{4} = |2 - \sqrt{5}| + \sqrt{4}$ (hoặc $\sqrt{5} - 2 + \sqrt{4}$ )

$= \sqrt{5} - 2 + 2 = \sqrt{5}$

Câu 4:

Thực hiện tính:

$\frac{1}{\sqrt{2} + \sqrt{3}} + \sqrt{2}$

Xem đáp án

$C = \frac{1}{\sqrt{2} + \sqrt{3}} + \sqrt{2} = \frac{\sqrt{2} - \sqrt{3}}{(\sqrt{2} + \sqrt{3}) (\sqrt{2} - \sqrt{3})} + \sqrt{2}$ (hoặc = $\sqrt{3} - \sqrt{2} + \sqrt{2}$ )

$= \frac{\sqrt{2} - \sqrt{3}}{2 - 3} + \sqrt{2} = \sqrt{3} - \sqrt{2} + \sqrt{2} = \sqrt{3}$

Câu 5:

Cho biểu thức

P = (\frac{1}{\sqrt{a} + 1} - \frac{1}{a + \sqrt{a}}) . \frac{a + 2 \sqrt{a} + 1}{\sqrt{a} - 1}

với a > 0 và

a \neq 1

a) Rút gọn biểu thức P.

b) Tính giá trị của P khi

a = 2 \sqrt{3 - \sqrt{5}} (3 + \sqrt{5}) (\sqrt{10} - \sqrt{2})

Xem đáp án

a) $P = \frac{\sqrt{a} - 1}{\sqrt{a} (\sqrt{a} + 1)} . \frac{a + 2 \sqrt{a} + 1}{\sqrt{a} - 1} = \frac{a + 2 \sqrt{a} + 1}{\sqrt{a} (\sqrt{a} + 1)}$

$= \frac{{(\sqrt{a} + 1)}^{2}}{\sqrt{a} (\sqrt{a} + 1)} = \frac{\sqrt{a} + 1}{\sqrt{a}} = \frac{a + \sqrt{a}}{a}$

b) $a = 2 \sqrt{3 - \sqrt{5}} . \sqrt{3 + \sqrt{5}} . \sqrt{3 + \sqrt{5} .} \sqrt{2} (\sqrt{5} - 1)$

$= 4 \sqrt{3 + \sqrt{5} .} \sqrt{2} (\sqrt{5} - 1)$

$a = 4 \sqrt{6 + 2 \sqrt{5}} . (\sqrt{5} - 1) = 4 (\sqrt{5} + 1) (\sqrt{5} - 1) = 16$

Tính được

P = \frac{5}{4}

Câu 6:

Tìm điều kiện của m để hàm số y = (m - 3)x + 4 là hàm số bậc nhất.

Xem đáp án

Để

y = (m - 3) x + 4

là hàm số bậc nhất thì

m - 3 \neq 0

\Rightarrow m \neq 3

Câu 7:

Vẽ đồ thị hàm số y = 2x - 3

Xem đáp án

Xác định được tọa độ hai điểm thuộc đồ thị hàm số (Ví dụ: A(0; -3) và B(2;1)).

Vẽ đồ thị hàm số y = 2x-3:

- Vẽ hệ trục tọa độ.

- Biểu diễn hai điểm trên hệ trục tọa độ.

- Vẽ đường thẳng qua hai điểm.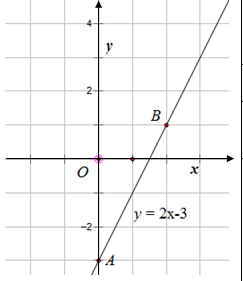

Câu 8:

Tìm m để đồ thị hàm số y = (m - 3)x + 4 cắt đồ thị hàm số y = 2x - 3 tại điểm có hoành độ bằng 1.

Xem đáp án

Gọi C(x₀; y₀) là tọa độ giao điểm. Có:

x₀ =1 Þ

y_{0} = 2.1 - 3 = - 1

y = (m - 3) x + 4

qua C(1; -1) có:

- 1 = m - 3 + 4 \Rightarrow m = - 2 .

Câu 9:

Vẽ tam giác ABC vuông tại A có AB = 4cm; AC = 5cm và AH là đường cao.

a) Tính độ dài đoạn thẳng AH.

b) Tính các tỉ số lượng giác: tanB, sinC.

c) Gọi E là hình chiếu của H trên AB và F là hình chiếu của H trên AC.

Chứng minh AE.AB = AF.AC

Xem đáp án

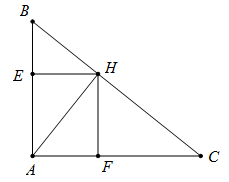
Vẽ tam giác ABC vuông tại A có AB = 4cm; AC = 5cm và AH là đường cao. (ảnh 1)

a) Có: $\frac{1}{{AH}^{2}} = \frac{1}{{AB}^{2}} + \frac{1}{{AC}^{2}}$ hay $\frac{1}{{AH}^{2}} = \frac{1}{4^{2}} + \frac{1}{5^{2}}$

${AH}^{2} = \frac{4^{2} {.5}^{2}}{4^{2} {+5}^{2}} \Rightarrow AH= \frac{20}{\sqrt{41}}$ ( $\approx 3, 12$ )

b) $tanB = \frac{AC}{AB} = \frac{5}{4}$ (= 1,25)

$s inC = \frac{AH}{AC} = \frac{20}{\sqrt{41}} : 5 = \frac{4}{\sqrt{41}}$ ( $\approx 0, 62$ )

c) DAHB vuông tại H có HE là đường cao nên AE. AB = AH²

Tương tự có AF.AC = AH² Þ AE. AB = AF.AC (cùng bằng AH²)

Câu 10:

Cho nửa đường tròn tâm O có đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc nửa đường tròn (M khác A và B). Đường thẳng qua M vuông góc với OM cắt Ax tại C và cắt By tại D.

a) Chứng minh CA = CM.

b) Chứng minh $\hat{MOB} = 2. \hat{MAO}$ , từ đó suy ra AM song song với OD.

c) Gọi N là giao điểm của AD và BC. Chứng minh đường thẳng MN vuông góc với đường thẳng AB.

Xem đáp án

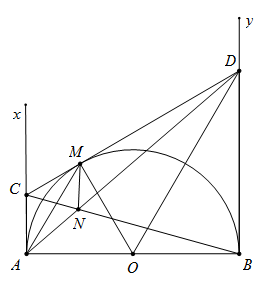
Cho nửa đường tròn tâm O có đường kính AB. Gọi Ax, By là các tia vuông góc với AB (ảnh 1)

a) CM ^ MO Þ CM là tiếp tuyến của (O)

CA ^ AO Þ CA là tiếp tuyến của (O).

Þ CM = CA (T.chất 2 tt cắt nhau).

b) DOMA cân tại O do OM = OA

$\Rightarrow \hat{MAO} = \hat{AMO}$

Mà $\hat{MOB} = \hat{MAO} + \hat{AMO}$ (góc ngoài)

$\Rightarrow \hat{MOB} = 2 \hat{MAO}$

Lí luận được BD là tiếp tuyến của (O)

Þ OD là phân giác của $\hat{MOB}$

Þ $\hat{MOB} = 2 \hat{DOB}$ Þ $\hat{MAO} = \hat{DOB}$

Þ AM // OD

c) AC // BD Þ

\frac{NC}{NB} = \frac{AC}{BD}

Mà AC = MC và BD = MD

\frac{NC}{NB} = \frac{MC}{MD}

Þ MN // BD Þ MN ^ AB

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập theo tuần Toán 9 - Tuần 17

Bài tập theo tuần Toán 9 - Tuần 17 - Đề 2

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương