Cho đường tròn (O), đường kính AB điểm D thuộc đường tròn. Gọi E là điểm đối xứng với A qua D.
a) Tam giác ABE là tam giác gì ? Vì sao ?
b) Gọi K là giao điểm của EB với (O). Chứng minh
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
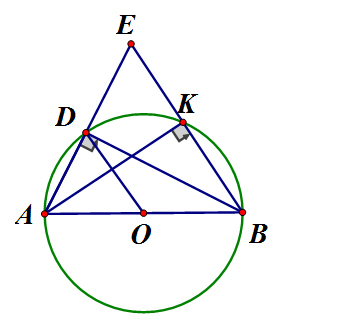
a) (góc nội tiếp chắn nửa đường tròn) có BD vừa là đường cao vừa là đường trung tuyến nên cân tại B
b) Xét là trung điểm AE, O là trung điểm AB nên OD là đường trung bình
Mà do là góc bội tiếp chắn nửa đường tròn
Cho tam giác ABC nội tiếp đường tròn (O), hai đường cao BD, CE cắt nhau tại H. Vẽ đường kính AF.
a) Tứ giác BFCH là hình gì ?
b) Gọi M là trung điểm của BC. Chứng minh rằng 3 điểm H, M, F thẳng hàng.
c) Chứng minh
Cho nửa đường tròn (O), đường kính AB = 2R và điểm C nằm ngoài nửa đường tròn và cùng phía với nửa mặt phẳng có bờ là đường thẳng AB và chứa nửa đường tròn. Đường thẳng CA cắt nửa đường tròn ở M, CB cắt nửa đường tròn ở N. Gọi H là giao điểm của AN và BM
a) Chứng minh :
b) Gọi I là trung điểm CH. Chứng minh MI là tiếp tuyến của nửa đường tròn (O).
Cho đường tròn (O) và hai dây AB, AC bằng nhau. Qua A vẽ một cát tuyến cắt dây BC ở D và cắt đường tròn (O) ở E. Chứng minh rằng:
Cho tam giác ABC có AB > AC. Trên cạnh AB lấy một điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp . Từ O lần lượt hạ các đường vuông góc OH, OK xuống BC, BD
a) Chứng minh rằng OH < OK
b) So sánh hai cung nhỏ BD, BC
Cho đường tròn (O) và hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung AC rồi vẽ tiếp tuyến đường tròn (O) tại M. Tiếp tuyến này cắt CD tại S. Chứng minh rằng
Tìm các giá trị của tham số m để nghiệm của hệ phương trình :
cũng là nghiệm của phương trình
Cho hệ phương trình (m là tham số)
Giải hệ phương trình khi m = -1
Cho đường tròn tâm O đường kính AB. Vẽ hai dây AM, BN song song với nhau sao cho Vẽ dây MD song song với AB. Dây DN cắt AB tại E. Từ E vẽ một đường thẳng song song với AM cắt đường thẳng DM tại C. Chứng minh:
a)
b) BC là tiếp tuyến của (O)