Cho ΔABC vuông tại A biết AB=6cm,BC=10cm. Đường phân giác ngoài của góc ngoài tại đỉnh B cắt tia CA tại E. Tính độ dài đoạn thẳng BE
A.BE=2√5cm
B.BE=6√5cm
C.BE=4√5cm
D.BE=5√5cm
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
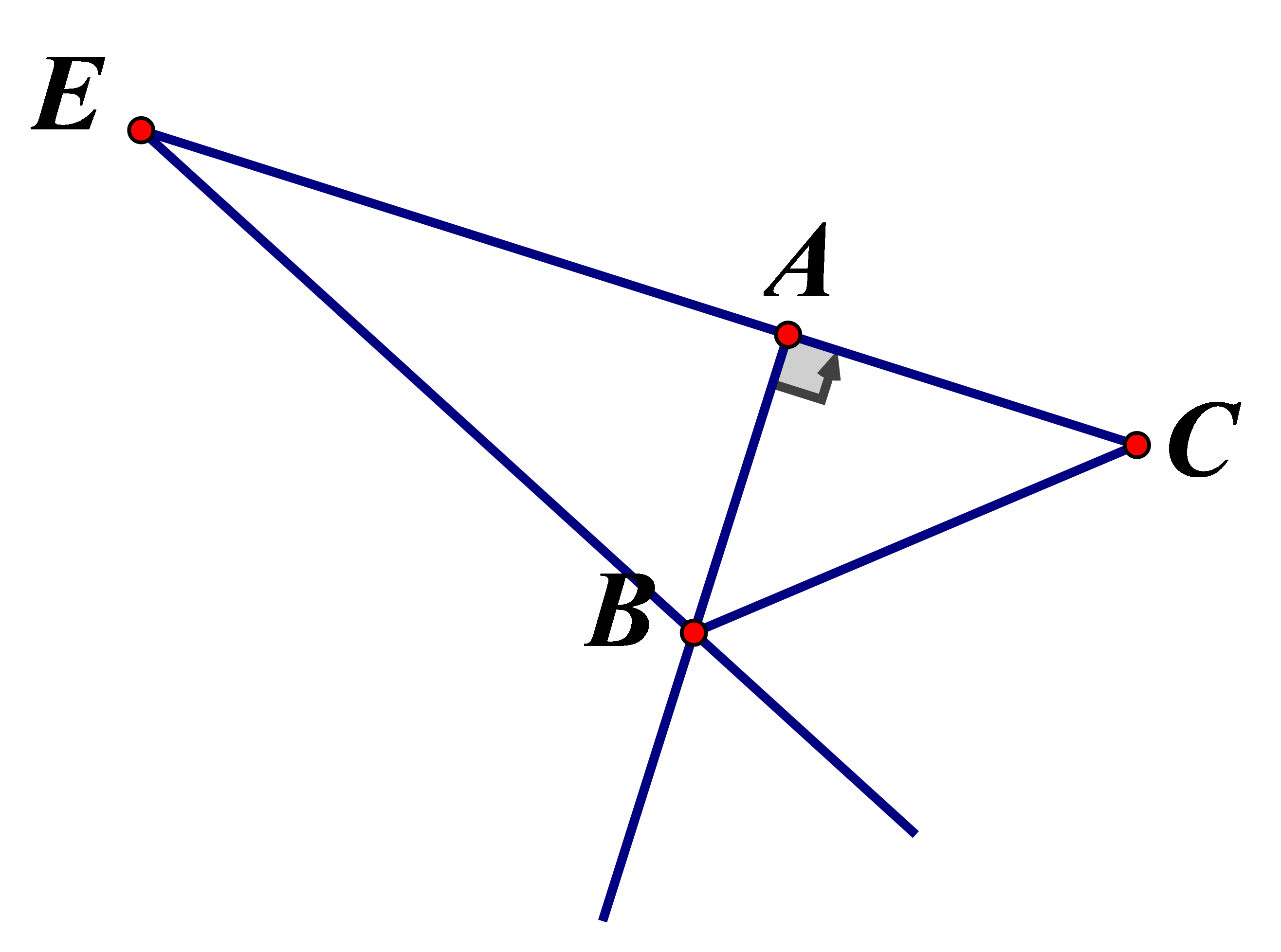
ΔABC vuông tại A ⇒AC=√BC2−AB2=√102−62=4(cm)
Vì BE là phân giác ngoài tại đỉnh B
⇒ECEA=BCBA=ECEC+AC=BCBA⇒EC.BA=BC.(EC+AC)
⇔EC.(BC−BA)=BC.AC⇔EC=BC.ACBA−BC=10.410−6=10cm
⇒BE=6√5
Chọn đáp án B
Tính diện tích của hình tam giác giới hạn bởi các đường thẳng y=−x+6,y=2x và trục Ox Biết rằng, mỗi đơn vị trên trục tọa độ có độ dài
Cho ΔABC có ∠A=900,AB=6,AC=8.Gọi M là trung điểm của BC,G là trọng tâm của ΔABC. Tính GM
Cho ΔABC cân tại A. Biết ∠ACB=300,AB=8cm. Tính độ dài đường tròn ngoại tiếp ΔABC
Với cùng số tiền mua 36 quyển vở loại I có thể mua được bao nhiêu quyển vở loại II.Biết giá tiền quyển vở loại II bằng75% giá tiền một quyển vở loại I.
Cho ΔABC vuông tại A, đường cao AH .Biết BHHC=916,AH=48cm. Tính độ dài cạnh AB:
Cho đường tròn (O;5cm), dây MN=8cm. Đoạn thẳng OI⊥MN(I∈MN) .Tính độ dài đoạn thẳng OI
Cho phương trình x2−2(m−3)x+2m−7=0(1) . Gọi hai nghiệm của phương trình (1) là x1,x2, tìm tất cả các giá trị của m để 1x1+1+1x2+1=m
Cho hình vuông ABCD có tâm O, cạnh 4cm. Vẽ hai đường tròn (O1;1cm) và (O2;1cm) tiếp xúc với hai cạnh AB,CD của hình vuông và tiếp xúc nhau tại O. Vẽ hai đường tròn (O3) và (O4) tiếp xúc với hai cạnh AD, BC của hình vuông và mỗi đường tròn đều tiếp xúc với cả hai đường tròn (O1) và (O2) . Tính tổng diện tích S của các hình tròn(O1),(O2),(O3),(O4)
Tìm tất cả các giá trị của a,b để hệ phương trình {ax+y=−5bx−ay=1 có nghiệm (x;y)=(2;1)
Cho ΔABC vuông tại A.Biết ∠B=600,AC=10cm. Khẳng định nào sau đây đúng ?
Cho ΔABC có ∠A=800 nội tiếp đường tròn (O;R) . Tính diện tích S của hình quạt tròn OBC (chứa cung nhỏ BC)
Cho ΔABC vuông tại A đường cao AH. Biết AC=4cm,BC=5cm. Tính độ dài đường cao AH