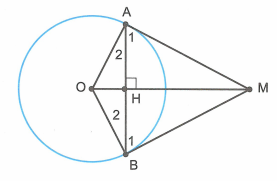
Cho đường tròn $\left(O;12\text{ cm}\right)$ và điểm M cách  một khoảng bằng 20 cm. Kẻ tiếp tuyến MA ( là tiếp điểm) và kẻ dây  vuông góc với OM. Chứng minh MB là tiếp tuyến của đường tròn (O).

Cho đường tròn (0; R) và điểm A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AE đến đường tròn (O) (với E là tiếp điểm). Vẽ dây EH vuông góc với AO tại M.

a) Cho biết bán kính R = 5cm, OM = 3cm. Tính độ dài dây EH.

b) Chứng minh AH là tiếp tuyến của đường tròn (O).

c) Đường thẳng qua O vuông góc với OA cắt AH tại B. Vẽ tiếp tuyến BF với đường tròn (O) (F là tiếp điểm). Chứng minh ba điểm E, O, F thẳng hàng và $BF.AE=R^2$.

d) Trên tia HB lấy điểm $I\left(I\ne B\right)$, qua I vẽ tiếp tuyến thứ hai với đường tròn (O) cắt các đường thẳng BF, AE lần lượt tại C và D. Vẽ đường thẳng IF cắt AE tại Q.

Chứng minh AE = DQ.

Cho đường tròn $\left(O;R\right)$ đường kính $AB$. Qua $A$ và $B$ vẽ lần lượt hai tiếp tuyến $\left(d\right)$ và $\left(d^{\text{'}}\right)$. Một đường thẳng qua $O$ cắt đường thẳng $\left(d\right)$ ở $M$ và $\left(d^{\text{'}}\right)$ ở $P$. Từ $O$ kẻ $Ox$ vuông góc với $MP$ và cắt $\left(d^{\text{'}}\right)$ ở $N$.

Cho tam giác $ABC$ có hai đường cao BD và $CE$ cắt nhau tại $H$.

a) Chứng minh rằng bốn điểm A, D, H , cùng nằm trên một đường tròn (gọi tâm của nó là O ).

b) Gọi M là trung điểm của $BC$. Chứng minh rằng ME là tiếp tuyến của đường tròn (O).