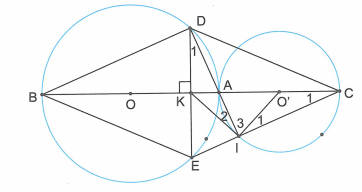
Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài tại A. Đường nối tâm OO’ cắt (O), (O’) lần lượt tại B, C. Dây DE của (O) vuông góc với BC tại trung điểm K của BC.
a) Chứng minh BDCE là hình thoi.
b) Gọi I là giao điểm của EC và (O’). Chứng minh D, A, I thẳng hàng.
c) Chứng minh KI là tiếp tuyến của (O’).
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Phân tích đề bài
c) KI là tiếp tuyến của (O’)
có
Giải chi tiết
a) Vì BC vuông góc với đường thẳng DE nên DK = EK (quan hệ đường kính và dây cung).
Mà BK = CK (giả thiết), do đó tứ giác BDCE là hình bình hành, lại có nên BDCE là hình thoi.
b) Vì tam giác BDA nội tiếp đường tròn (O) có BA là đường kính nên vuông tại D.
Gọi I’ là giao điểm của DA với CE thì (vì so le trong với ). (1)
Lại có vuông tại I ( nội tiếp đường tròn (O’) có AC là đường kính)
. (2)
Từ (1) và (2) suy ra I = I’. Vậy D, A, I thẳng hàng.
c) Vì vuông tại I có IK là trung tuyến ứng với cạnh huyền DE nên KD = KI = KE.
. (3)
Lại có (cùng phụ với ). (4)
(vì IO’ = CO’ là bán kính của đường tròn (O’)). (5)
Từ (3), (4), (5) suy ra hay . Do đó KI vuông góc với bán kính O’I của đường tròn (O’). Vậy KI là tiếp tuyến của đường tròn (O’).
Cho hai đường tròn cắt nhau tại H và K, đường thẳng cắt tại A, cắt tại B, cắt tại C, cắt tại D. Chứng minh ba đường thẳng AC, BD, HK đồng quy tại một điểm.
Cho hai đường tròn (O)và (O’) tiếp xúc ngoài tại I. Kẻ tiếp tuyến chung ngoài MN với M thuộc (O) và N thuộc (O’). Gọi P là điểm đối xứng với M qua OO’, Q là điểm đối xứng với N qua OO’. Chứng minh rằng:
a) MNPQ là hình thang cân.
b) PQ là tiếp tuyến chung của hai đường tròn (O)và (O’).
c) .