Cho hình thoi ABCD có ˆA=60∘. Qua C kẻ đường thẳng d không cắt hình thoi nhưng cắt đường thẳng AB tại E và cắt đường thẳng AD tại F.
Chứng minh ΔDCF∼ΔAEF
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
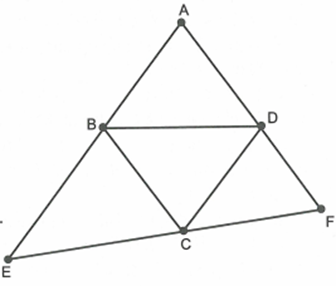
Chứng minh tương tự bài trước
Cho tam giác ABC có AB=18cm,AC=24cm,BC=30cm. Gọi M là trung điểm của BC. Qua M kẻ đường vuông góc với BC cắt AB, AC lần lượt ở D, E.
Chứng minh rằng: ΔABC∼ΔMDC
Cho tam giác ABC vuông tại B. Đường phân giác AD. Biết AB=6cm,AC=10cm.
Tính BD và CD
Cho tam giác ABC, AD là tia phân giác của góc A; AB<AC. Trên tia đối của tia DA lấy điểm I sao cho ^ACI=^BDA. Chứng minh rằng
AD2=AB.AC−BD.CD
Cho tam giác ABC cân tại A, M là trung điểm của BC. Lấy các điểm D và E trên AB, AC sao cho ^DME=ˆB
Chứng minh rằng ΔBDM∼ΔCME
Cho tam giác ABC có ba góc nhọn, đường cao AH (H∈BC). Kẻ tại D, HE⊥AC tại E.
Chứng minh ΔAHB∼ΔADH,ΔAHC∼ΔAEH
Cho tứ giác ABCD có diện tích 36 cm2, trong đó diện tích ΔABC là 11 cm2. Qua điểm B kẻ đường thẳng song song với AC cắt AD ở M, cắt CD ở N. Tính diện tích ΔMND.
Cho tam giác ABC có AB=6cm,AC=9cm,BC=12cm và ΔMNP có MN=24cm,NP=18cm,MP=12cm.
Tính tỉ số diện tích của hai tam giác trên.
Cho tam giác ABC vuông tại A có AB=20cm,BC=25cm. Gọi M là điểm thuộc cạnh AB.
Chứng minh AC.AD=AM.AB
Cho tam giác ABC vuông tại B. Đường phân giác AD. Biết AB=6cm,AC=10cm.
Chứng minh AK∥DF
Cho tam giác ABC vuông tại A. Đường phân giác của góc A cắt cạnh huyền BC tại D. Qua D kẻ đường thẳng vuông góc với BC và cắt AC tại E.
Chứng minh DE=DB
Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
Chứng minh rằng ΔAFE∼ΔACB
Cho hình thang ABCD (AB∥CD) có ^DAB=^DBC và AD=5cm,AB=3cm,BC=9cm.
Chứng minh ΔDAB∼ΔCBD.
Cho tam giác ΔABC có AB=9cm,AC=6cm. Điểm D nằm trên cạnh AB sao cho AD=2cm. Gọi E là trung điểm của AC. Chứng minh ΔAED∼ΔABC
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB=4cm,AC=3cm.
Chứng minh ΔHAC∼ΔABC.
Cho tam giác ABC cân tại A, M là trung điểm của BC. Lấy các điểm D và E trên AB, AC sao cho ^DME=ˆB
Chứng minh rằng ΔMDE∼ΔDBM