Câu hỏi:

22/07/2024 65

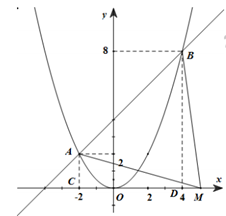
Cho hai hàm số $y = \frac{1}{2} x^{2}$ và đồ thị hàm số (P) và $y = x + 4$ có đồ thị (d). Gọi A,B là các giao điểm của hai đồ thị (P) và (d). Biết rằng đơn vị đo trên các trục tọa độ là xentimét, tìm tất cả các điểm M trên tia Ox sao cho diện tích tam giác MAB bằng 30 cm².

Xem lời giải

Bắt Đầu Thi Thử

Trả lời:

Giải bởi qa.haylamdo.com

Xét phương trình hoành độ giao điểm của (P) và (d) là:

$\frac{1}{2} x^{2} = x + 4 \Leftrightarrow x^{2} - 2 x - 8 = 0$

Phương trình có 2 nghiệm phân biệt: $x = 4; x = - 2$

Với $x = - 2$ ta có $y = 2 \Rightarrow A (- 2; 2)$

Với $x = 4$ ta có $y = 8 \Rightarrow B (4; 8)$

Gọi $M (m; 0)$ thuộc tia $O x (m > 0)$ Gọi $C (- 2; 0), D (4; 0)$

Xét hai trường hợp:

Trường hợp 1: M thuộc đoạn OD: Ta có $S_{A M B} = S_{A B D C} - S_{A C M} - S_{B D M}$

Có là hình thang, $A C = 2 c m, B D = 8 c m, C D = 6 c m$

⇒ $S_{A B D C} = \frac{(2 + 8) \cdot 6}{2} = 30 ({cm}^{2})$

Suy ra $S_{A M B} < 30$ cm² (loại)

Trường hợp 2: M thuộc tia Dx $(M \neq D) \Rightarrow m > 4$

Ta có : $S_{A M B} = S_{A B D C} - S_{A C M} + S_{B D M}$

Có $S_{A B C D} = 30 c m^{2}, M C = m + 2 (c m), M D = m - 4 (c m)$

Suy ra

$S_{A C M} = \frac{1}{2} A C . C M = \frac{1}{2} .2. (m + 2) = m + 2 (c m^{2})$

$S_{B D M} = \frac{1}{2} B D . D M = \frac{1}{2} .8. (m - 4) = 4 (m - 4) (c m^{2})$

$\Rightarrow S_{A M B} = 30 c m^{2} \Leftrightarrow S_{A C M} = S_{B D M} \Leftrightarrow m + 2 = 4 (m - 4) \Leftrightarrow m = 6$

m = 6 (thỏa mãn). Vậy $M (6; 0)$ là điểm cần tìm.

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho Parabol $(P) : y = x^{2}$ và đường thẳng $d : y = (2 m - 1) x - m + 2$ (m là tham số)
Chứng minh rằng với mọi m đường thẳng d luôn cắt (P) tại hai điểm phân biệt

Xem đáp án » 19/10/2022 531

Câu 2:

Cho parabol $(P) : y = x^{2}$ và đường thẳng (d) có phương trình: $y = 2 (m + 1) x - 3 m + 2$ .

Chứng minh (P) và (d) luôn cắt nhau tại 2 điểm phân biệt A và B với mọi m.

Xem đáp án » 19/10/2022 223

Câu 3:

Trong mặt phẳng tọa độ Oxy cho đường thẳng $(d) : y = x + m - 1$ và parabol $(P) : y = x^{2}$ . Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là $x_{1}$ $x_{2}$ thỏa mãn: $4 (\frac{1}{x_{1}} + \frac{1}{x_{2}}) - x_{1} x_{2} + 3 = 0$ .

Xem đáp án » 19/10/2022 196

Câu 4:

Trong mặt phẳng tọa độ Oxy cho đường thẳng $(d) : y = 3 x + m - 1$ và parabol $(P) : y = x^{2}$ . Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt với mọi m.

Xem đáp án » 19/10/2022 180

Câu 5:

Trong mặt phẳng tọa độ Oxy cho đường thẳng $(d) : y = 3 x + m - 1$ và parabol $(P) : y = x^{2}$ . Gọi $x_{1}, x_{2}$ là hoành độ các giao điểm của (d) và (P). Tìm m để $(x_{1} + 1) (x_{2} + 1) = 1$

Xem đáp án » 19/10/2022 173

Câu 6:

Cho đường thẳng (d) có phương trình $y = x + 2$ và parabol (P) có phương trình $y = x^{2}$ . Vẽ đường thẳng (d) và parabol (P) trên cùng hệ trục tọa độ .

Xem đáp án » 19/10/2022 159

Câu 7:

Trong mặt phẳng tọa độ Oxy cho Parabol $(P) : y = - x^{2}$ và đường thẳng $(d) : y = 3 m x - 3$ (với m là tham số). Xác định các giá trị của m để (d) cắt (P) tại hai điểm phân biệt sao cho tổng 2 tung độ của hai giao điểm đó bằng -10

Xem đáp án » 19/10/2022 158

Câu 8:

Cho parabol $(P) : y = x^{2}$ và đường thẳng $(d) : y = 2 (m + 3) x - 2 m + 2$ (m là tham số).

Chứng minh rằng: với mọi m parabol (P) và đường thẳng (d) cắt nhau tại hai điểm phân biệt. Tìm m sao cho hai giao điểm đó có hoành độ dương.

Xem đáp án » 19/10/2022 155

Câu 9:

Cho parabol $(P) : y = x^{2}$ và đường thẳng $(d) : y = - 2 a x - 4 a$ (với a là tham số )

Tìm tất cả các giá trị của a để đường thẳng (d) cắt (P) taị hai điểm phân biệt có hoành độ $x_{1}; x_{2}$ thỏa mãn $|x_{1}| + |x_{2}| = 3$ .

Xem đáp án » 19/10/2022 153

Câu 10:

Cho parabol $(P) : y = x^{2}$ và đường thẳng (d) có phương trình: $y = 2 (m + 1) x - 3 m + 2$ .Tìm tọa độ giao điểm của (P) và (d) với m=3.

Xem đáp án » 19/10/2022 147

Câu 11:

Cho hai hàm số $y = x^{2}$ và $y = m x + 4$ , với m là tham số.
Chứng minh rằng với mọi giá trị m, đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt $A_{1} (x_{1}; y_{1})$ và $A_{2} (x_{2}; y_{2})$ Tìm tất cả các giá trị của m sao cho ${(y_{1})}^{2} + {(y_{2})}^{2} = 7^{2}$ .

Xem đáp án » 19/10/2022 146

Câu 12:

Trong mặt phẳng với hệ tọa độ , cho parabol $(P) : y = \frac{1}{2} x^{2}$ và đường thẳng $(d) : y = \frac{1}{4} x + \frac{3}{2}$

Gọi $A (x_{1}; y_{1})$ và $B (x_{2}; y_{2})$ lần lượt là các giao điểm của (P) với (d). Tính giá trị biểu thức $T = \frac{x_{1} + x_{2}}{y_{1} + y_{2}}$ .

Xem đáp án » 19/10/2022 142

Câu 13:

Trong mặt phẳng tọa độ $O x y$ cho đường thẳng $(d) : y = m x - 3$ tham số m và Parabol $(P) : y = x^{2}$
Tìm m để đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là $x_{1}; x_{2}$ thỏa mãn $|x_{1} - x_{2}| = 2$ .

Xem đáp án » 19/10/2022 142

Câu 14:

Cho hàm số $y = - \frac{1}{2} x^{2}$ có đồ thị (P) .Cho đường thẳng $y = m x + n (Δ)$ . Tìm m,n để đường thẳng $(Δ)$ song song với đường thẳng $y = - 2 x + 5 (d)$ và có duy nhất một điểm chung với đồ thị $(P)$ .

Xem đáp án » 19/10/2022 139

Câu 15:

Cho hai hàm số $y = x^{2}$ và $y = m x + 4$ , với m là tham số.

Khi m=3, tìm tọa độ các giao điểm của hai đồ thị hàm số trên.

Xem đáp án » 19/10/2022 134

Xem thêm các câu hỏi khác »

Đề thi liên quan

Xem thêm »

Trắc nghiệm Toán 9 (Có đáp án): Căn thức bậc hai

2 đề 15310 lượt thi Thi thử
Bộ 30 đề thi vào 10 môn Toán có lời giải chi tiết

29 đề 6164 lượt thi Thi thử
Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

31 đề 4920 lượt thi Thi thử
Tổng hợp đề thi chính thức vào 10 môn Toán năm 2021 có đáp án (Phần 1)

31 đề 4616 lượt thi Thi thử
Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án

17 đề 4477 lượt thi Thi thử
Trắc nghiệm Toán 9 Bài 1 (có đáp án): Căn bậc hai

2 đề 3788 lượt thi Thi thử
Đề kiểm tra 15 phút Toán 9 Chương 1 Đại Số (có đáp án)

7 đề 3688 lượt thi Thi thử
Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)

22 đề 3306 lượt thi Thi thử
Trắc nghiệm Toán 9 Bài 2 (có đáp án): Căn thức bậc hai và hằng đẳng thức

2 đề 3265 lượt thi Thi thử
Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án

6 đề 2963 lượt thi Thi thử

Xem thêm »

Hỏi bài

Câu hỏi mới nhất

Xem thêm »

CHỌN BỘ SÁCH BẠN MUỐN XEM

Câu hỏi:

Trả lời:

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho Parabol (P):y=x2 và đường thẳng d:y=(2m−1)x−m+2 (m là tham số) Chứng minh rằng với mọi m đường thẳng d luôn cắt (P) tại hai điểm phân biệt

Câu 2:

Cho parabol (P):y=x2 và đường thẳng (d) có phương trình: y=2(m+1)x−3m+2 . Chứng minh (P) và (d) luôn cắt nhau tại 2 điểm phân biệt A và B với mọi m.

Câu 3:

Trong mặt phẳng tọa độ Oxy cho đường thẳng (d):y=x+m−1 và parabol (P):y=x2. Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là x1 x2 thỏa mãn: 41x1+1x2−x1x2+3=0 .

Câu 4:

Trong mặt phẳng tọa độ Oxy cho đường thẳng (d):y=3x+m−1 và parabol (P):y=x2. Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt với mọi m.

Câu 5:

Trong mặt phẳng tọa độ Oxy cho đường thẳng (d):y=3x+m−1 và parabol (P):y=x2. Gọi x1,x2 là hoành độ các giao điểm của (d) và (P). Tìm m để x1+1x2+1=1

Câu 6:

Cho đường thẳng (d) có phương trình y=x+2 và parabol (P) có phương trình y=x2. Vẽ đường thẳng (d) và parabol (P) trên cùng hệ trục tọa độ .

Câu 7:

Cho Parabol $(P) : y = x^{2}$ và đường thẳng $d : y = (2 m - 1) x - m + 2$ (m là tham số)
Chứng minh rằng với mọi m đường thẳng d luôn cắt (P) tại hai điểm phân biệt

Cho parabol $(P) : y = x^{2}$ và đường thẳng (d) có phương trình: $y = 2 (m + 1) x - 3 m + 2$ .

Chứng minh (P) và (d) luôn cắt nhau tại 2 điểm phân biệt A và B với mọi m.

Trong mặt phẳng tọa độ Oxy cho đường thẳng $(d) : y = 3 x + m - 1$ và parabol $(P) : y = x^{2}$ . Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt với mọi m.

Trong mặt phẳng tọa độ Oxy cho đường thẳng $(d) : y = 3 x + m - 1$ và parabol $(P) : y = x^{2}$ . Gọi $x_{1}, x_{2}$ là hoành độ các giao điểm của (d) và (P). Tìm m để $(x_{1} + 1) (x_{2} + 1) = 1$

Cho đường thẳng (d) có phương trình $y = x + 2$ và parabol (P) có phương trình $y = x^{2}$ . Vẽ đường thẳng (d) và parabol (P) trên cùng hệ trục tọa độ .