 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Cách 1.
Ta có: BC ^ SA, BC ^ AB Þ BC ^ SB.
Ta có: = 90°.
Khi đó 4 điểm S, A, B, C nằm trên mặt cầu đường kính SC.
Bán kính mặt cầu R = = 2a.
Diện tích mặt cầu ngoại tiếp hình chóp S = 4π(2a)2 = 16πa2.Cách 2.
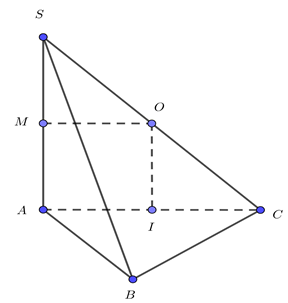
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC, do tam giác ABC vuông tại B nên I là trung điểm của AC.
Qua I dựng đường thẳng d vuông góc với (ABC) nên ta được d // SA.
Trong tam giác SAC, dựng đường trung trực của SA cắt d tại O là tâm mặt cầu ngoại tiếp hình chóp S. ABC.
Ta tính được AC = 2a, SC = 4a.
Bán kính mặt cầu R = OA = = 2a.
Diện tích mặt cầu ngoại tiếp hình chóp S.ABC là:
S = 4π(2a)2 = 16πa2.