Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(−2; −2; 1), A(1; 2; −3) và đường thẳng d : . Gọi = (1; a; b) là một vectơ chỉ phương của đường thẳng ∆ đi qua M, ∆ vuông góc với đường thẳng d đồng thời cách điểm A một khoảng nhỏ nhất. Giá trị của a + 2b là
A.1
B. 2
C. 3
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án đúng là: D
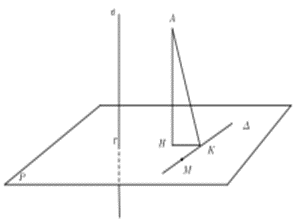
Gọi (P) là mặt phẳng đi qua M và vuông góc với d, khi đó (P) chứa ∆
Mặt phẳng (P) qua M(−2; −2; 1) và có vectơ pháp tuyến = = (2; 2; −1) nên có phương trình : (P) : 2x + 2y – z + 9 = 0
Gọi H, K lần lượt là hình chiếu của A lên (P) và ∆. Khi đó: AK ≥ AH nên AK min khi
K ≡ H. Đường thẳng AH đi qua A(1; 2; −3) và có vectơ chỉ phương = (2; 2; −1) nên AH có phương trình tham số:
H ∈ AH Þ H(1 + 2t; 2 + 2t; −3 – t)
H ∈ (P) Þ 2(1 + 2t) + 2(2 + 2t) –(−3 – t) + 9 = 0 Þ H(−3; −2; −1)
Nên = = (1; 0; 2)
Vậy a = 0; b = 2 Þ a + 2b = 4
Trong không gian với hệ tọa độ Oxyz, cho (S) : x2 + y2 + z2 – 4x – 2y + 10z – 14 = 0. Mặt phẳng (P) : −x + 4z + 5 = 0 cắt mặt cầu (S) theo một đường tròn (C). Tọa độ tâm H của (C) là
Cho hàm số f(x) = ax3 + bx2 – 36x + c (a≠ 0; a, b, c ∈ ℝ) có hai điểm cực trị là −6 và 2. Gọi y = g(x) là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = f(x). Diện tích hình phẳng giới hạn bởi hai đường thẳng y = f(x) và y = g(x) bằng
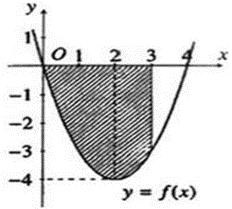
Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới. Diện tích S của miền được tô đậm như hình vẽ được tính theo công thức nào sau đây?
Trong không gian hệ tọa độ Oxyz, cho mặt phẳng (α) : 2x + 2y – z – 6 = 0. Gọi mặt phẳng (β) : x + y + cz + d = 0 không qua O, song song với mặt phẳng (α) và d((α),(β)) = 2. Tính c.d?
Gọi S là diện tích hình phẳng giới hạn bởi hai đường y = và y = 4 – x. Tính S
Trong không gian, cắt vật thể bởi hai mặt phẳng (P) : x = −1 và (Q) : x = 2. Biết một mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x (−1 ≤ x ≤ 2) cắt theo thiết diện là một hình vuông có cạnh bằng 6 – x. Thể tích của vật thể giới hạn bởi hai đường thẳng (P), (Q) bằng
Biết phương trình z2 + mz + n = 0 (m; n ∈ ℝ) có một nghiệm là 1 – 3i. Tính n + 3m
Trong không gian với hệ tọa độ Oxyz, cho điểm M(−2; 1; 8). Gọi H là hình chiếu vuông góc của M trên mặt phẳng (Oxy). Tọa độ của điểm H là
Trong không gian Oxyz, cho mặt phẳng (P): 2x – 2y + z + 6 = 0. Khoảng cách từ gốc tọa độ đến mặt phẳng (P) bằng
Trong không gian Oxyz, cho đường thẳng d có phương trình (t ∈ ℝ). Hỏi đường thẳng d đi qua điểm nào sau đây?
Trong không gian Oxyz, cho mặt cầu (S) : x2 + y2 + z2 + 2x + 4y – 6z – 1 = 0. Tâm của mặt cầu (S) có tọa độ là:
Trong không gian Oxyz, gọi M(a; b; c) là giao điểm của đường thẳng d : và mặt phẳng (P) : 2x + 3y – 4z + 4 = 0. Tính T = a + b + c