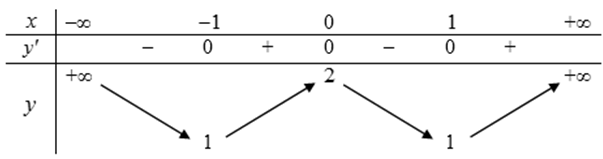
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên.
A. Hàm số đồng biến trên các khoảng (-1;0) và (1;+∞)
B. f (1) và f(-1) được gọi là giá trị cực tiểu của hàm số
C. x0 = 1 được gọi là điểm cực tiểu của hàm số
D. M(0;2) được gọi là điểm cực đại của hàm số
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án D.
* Hàm số đồng biến trên (-1;0) và (1;+∞) => A đúng.
* x = -1; x = 1 là các điểm cực tiểu của hàm số, f(-1); f(1) là các giá trị cực tiểu của hàm số => B,C đúng.
* M(0;2) được gọi là điểm cực tiểu của đồ thị hàm số => D sai
Cho hàm số y = x4 – 2x2 – 1. Tìm số giao điểm của đồ thị hàm số với trục Ox:
Số giao điểm của trục hoành và đồ thị hàm số y = -x4 + 2x2 + 3 là:
Cho hàm số y = x4 – 4x2 – 2 có đồ thị (C) và đồ thị (P) : y = 1- x2. Số giao điểm của (P) và đồ thị (C) là
Tìm số giao điểm của đồ thị (C): y = x3 + x – 2 và đường thẳng y = x – 1
Đồ thị của hàm số y = -x3 + 3x2 + 2x – 1 và đồ thị của hàm số y = 3x2 – 2x – 1 có tất cả bao nhiêu điểm chung?
Tìm số giao điểm của đồ thị hàm số y = x4 – 2x2 và đồ thị hàm số y = x2 – 2
Tìm số giao điểm của đồ thị hàm số y = (x – 2)(x2 + x + 1) và trục hoành.
Tọa độ giao điểm có hoành độ nhỏ hơn 1 của đường (C): và đường thẳng (d): y = x + 1 là:
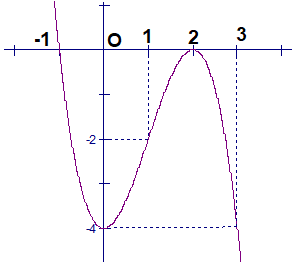
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên
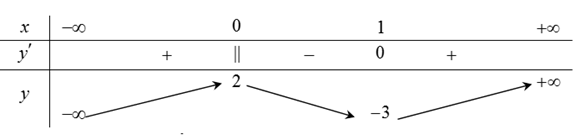
Khẳng định nào sau đây là khẳng định đúng
Cho hàm số y = f(x) xác định, liên tục trên R và có đồ thị là đường cong trong hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng?