Cho số phức z và w thỏa mãn z+w=3+4i và .
Tìm giá trị lớn nhất của biểu thức .
A. maxT=
B. maxT=14
C. maxT=4
D. maxT=
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án D
Đặt ![]() theo giả thiết ta có:
theo giả thiết ta có:
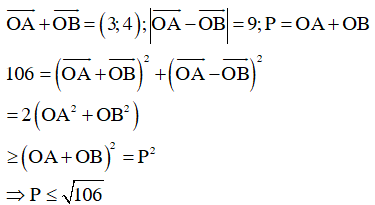
Tổng quát: Với 2 số thực thõa mãn ![]()
Khi đó ![]()
Cho số phức z thỏa mãn z(2-i)+13i=1. Tính mô đun của số phức z.
Cho hai số phức và .
Tính tổng phần thực và phần ảo của số phức .
Gọi S là tập hợp các số thực m sao cho với mỗi có đúng một số phức thỏa mãn và là số thuần ảo. Tính tổng của các phần tử của tập S.
Cho i là đơn vị ảo. Gọi S là tập hợp các số nguyên dương n có 2 chữ số thỏa mãn là số nguyên dương. Số phần tử của S là
Trong tập các số phức, cho phương trình (1). Gọi là một giá trị của m để phương trình (1) có hai nghiệm phân biệt thỏa mãn Hỏi trong khoảng (0;20) có bao nhiêu giá trị m ?
Cho số phức z thỏa mãn điều kiện .
Tìm giá trị lớn nhất của biểu thức
Cho số phức z thỏa mãn là số thực và với
Gọi là một giá trị của m để có đúng một số phức thỏa mãn bài toán.
Khi đó