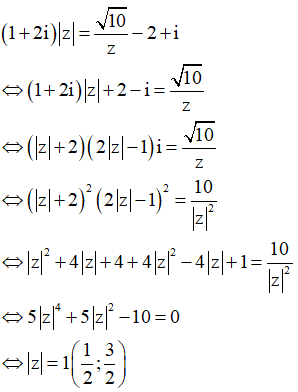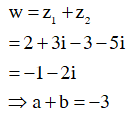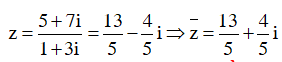Bài tập Số phức cơ bản, nâng cao có lời giải (P4)
-
3791 lượt thi
-
25 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho số phức thỏa mãn và
Giá trị lớn nhất của là
Đáp án C
Phương pháp: Gọi ![]() là số phức cần tìm. Sử dụng giả thiết để đưa ra một hệ điều kiện đẳng thức, bất đẳng thức cho a,b. Sử dụng điều kiện trên để đánh giá và tìm giá trị lớn nhất của P.
là số phức cần tìm. Sử dụng giả thiết để đưa ra một hệ điều kiện đẳng thức, bất đẳng thức cho a,b. Sử dụng điều kiện trên để đánh giá và tìm giá trị lớn nhất của P.
Lời giải chi tiết.
Giả sử số phức thỏa mãn yêu cầu bài toán có dạng ![]() Khi đó ta có
Khi đó ta có
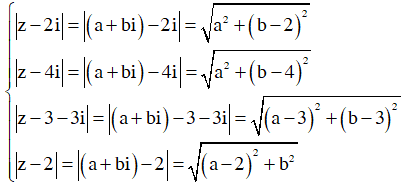
Từ giả thiết ta suy ra
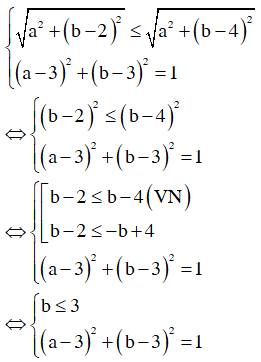
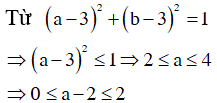
Do đó ![]()
Đẳng thức xảy ra khi và chỉ khi
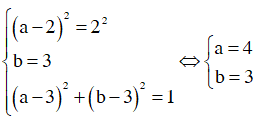
Chú ý. Đối với bài toán liên quan tới cực trị học sinh thường mắc phải sai lầm là quên tìm giá trị để cực trị xảy ra. Điều này có thể dẫn tới việc tìm sai giá trị lớn nhất nhỏ nhất
Câu 2:
Trong tập các số phức, cho phương trình (1). Gọi là một giá trị của m để phương trình (1) có hai nghiệm phân biệt thỏa mãn Hỏi trong khoảng (0;20) có bao nhiêu giá trị m ?
Đáp án D
Phương pháp
Biện luận để tìm trực tiếp nghiệm . Sử dụng giả thiết để tìm ra giá trị
Lời giải chi tiết.
Viết lại phương trình đã cho thành ![]()
Nếu Hay phương trình chỉ có một nghiệm. (Loại)
Nếu thì phương trình đã cho có hai nghiệm thực ![]()
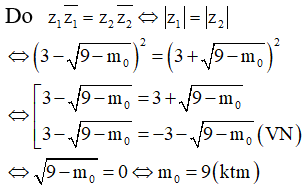
Nếu thì phương trình đã cho có hai nghiệm phức liên hợp là
![]()
Khi đó ![]()
Do đó thỏa mãn yêu cầu bài toán.
Do bài toán đòi hỏi nên ![]()
Vậy có 10 giá trị thỏa mãn.
Câu 3:
Gọi số phức thỏa mãn và có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng
Đáp án C
Phương pháp
Gọi số phức đã cho có dạng ![]() . Sử dụng giả thiết để đưa ra một hệ cho a, b giải trực tiếp hệ này để tìm a, b
. Sử dụng giả thiết để đưa ra một hệ cho a, b giải trực tiếp hệ này để tìm a, b
Lời giải chi tiết.
Ta có: ![]()
Do z không là số thực nên ta phải có (2)
Ta lại có
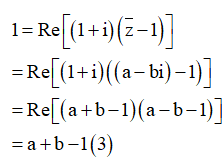
Từ (1), (2), (3) ta có hệ
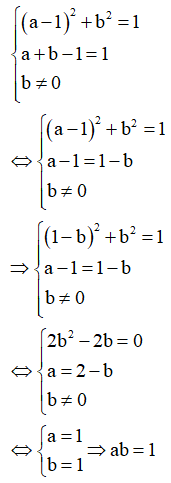
Câu 4:
Cho số phức z thỏa mãn z(2-i)+13i=1. Tính mô đun của số phức z.
Đáp án B
Phương pháp
Từ giả thiết ta biến đổi để tìm được công thức của z. Dùng định nghĩa để tìm
Lời giải chi tiết.
Ta có:
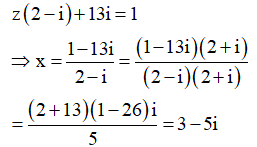
Do đó ![]()
Câu 5:
Cho số phức z thỏa mãn là số thực và với
Gọi là một giá trị của m để có đúng một số phức thỏa mãn bài toán.
Khi đó
Đáp án D
Phương pháp.Sử dụng giả thiết để tìm được ![]()
Thay vào ![]() và sử dụng yêu cầu bài toán để biện luận và tìm giá trị của
và sử dụng yêu cầu bài toán để biện luận và tìm giá trị của
Lời giải chi tiết.
Giả sử ![]() . Khi đó ta có
. Khi đó ta có
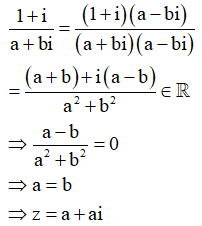
Thay vào ![]() Ta nhận được
Ta nhận được
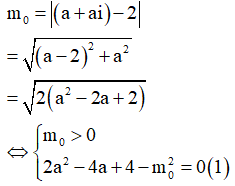
Để có đúng một nghiệm phức thỏa mãn bài toán thì phương trình (1) phải có duy nhất một nghiệm a.
Khi đó phương trình (1) phải thỏa mãn
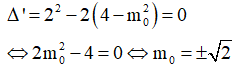
Kết hợp với điều kiện ![]() ta suy ra giá trị cần tìm là
ta suy ra giá trị cần tìm là ![]()
Sai lầm.Một bộ phận nhỏ học sinh vẫn có thể quên đưa ra điều kiện ![]() nên hai nghiệm là
nên hai nghiệm là ![]()
Câu 6:
Trong mặt phẳng phức, gọi M là điểm biểu diễn cho số phức với
Chọn kết luận đúng
Đáp án C
Phương pháp.
Tính trực tiếp ![]()
Lời giải chi tiết.
Ta có
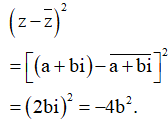
Do ![]()
Do đó M có phần thực âm, phần ảo bằng 0, nên thuộc tia đối của tia Ox.
Câu 7:
Trong tập các số phức, gọi là hai nghiệm của phương trình với có thành phần ảo dương. Cho số phức z thỏa mãn . Giá trị nhỏ nhất của là
Đáp án A
Phương pháp.
Giả sử ![]() Giả phương trình ban đầu để tìm được nghiệm Sử dụng giả thiết để đánh giá cho cho b. Đưa
Giả phương trình ban đầu để tìm được nghiệm Sử dụng giả thiết để đánh giá cho cho b. Đưa ![]() về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
Lời giải chi tiết.
Tính toán ta tìm được hai nghiệm 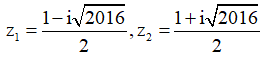
Giả sử ![]() . Từ
. Từ ![]() ta suy ra
ta suy ra
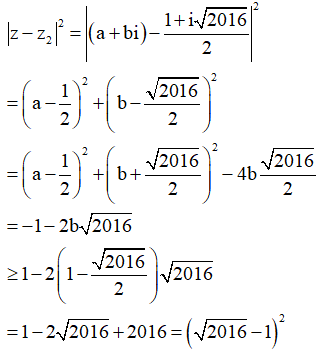
Áp dụng (1) ta nhận được
Do đó giá trị nhỏ nhất của ![]() là
là
Đạt được khi và chỉ khi ![]()
Câu 8:
Gọi S là tập hợp các số thực m sao cho với mỗi có đúng một số phức thỏa mãn và là số thuần ảo. Tính tổng của các phần tử của tập S.
Đáp án B
Phương pháp.
Gọi ![]() . Sử dụng giả thiết để tìm a, bsuy ra giá trị của z. Sử dụng kết quả này để tìm giá trị của m và kết luận.
. Sử dụng giả thiết để tìm a, bsuy ra giá trị của z. Sử dụng kết quả này để tìm giá trị của m và kết luận.
Lời giải chi tiết.
Giả sử ![]() Khi đó ta có
Khi đó ta có
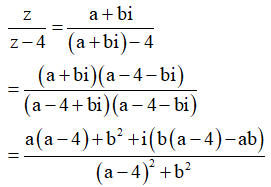
Để ![]() là số thuần ảo thì ta phải có
là số thuần ảo thì ta phải có
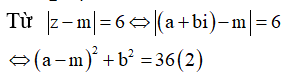
Từ (1) suy ra ![]() thay vào (2) ta nhận được
thay vào (2) ta nhận được
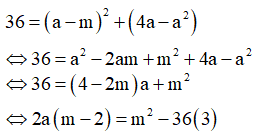
Nếu m=2 thì (3) vô nghiệm
Nếu m2 thì từ (3) suy ra ![]()
Vì ![]() nên để có duy nhất một số phức z thỏa mãn điều kiện đã cho thì b=0
nên để có duy nhất một số phức z thỏa mãn điều kiện đã cho thì b=0
Ta nhận được a=0 hoặc a=4
với a=4 thì z=a+bi=4. Loại vì ![]() là số thuần ảo
là số thuần ảo
vậy a=b=0z=0. Khi đó ![]()
Tổng các phần tử của S là 6+(-6)=0
Câu 9:
Tìm số phức z thỏa mãn và là số thực
Đáp án D
Phương pháp.
Gọi ![]() . Sử dụng giả thiết để tìm a, bsuy ra giá trị của z.
. Sử dụng giả thiết để tìm a, bsuy ra giá trị của z.
Lời giải chi tiết.
Giả sử ![]() .Khi đó ta có
.Khi đó ta có
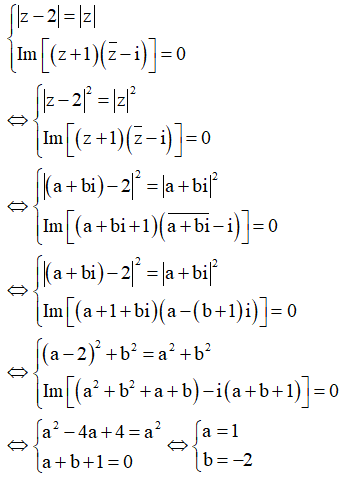
Vậy z=a+bi=1-2i
Sai lầm.Một số học sinh có thể nhớ nhầm thành do đó quá trình tính toán kết quả sẽ bị sai.
Câu 13:
Cho số phức z và w thỏa mãn z+w=3+4i và .
Tìm giá trị lớn nhất của biểu thức .
Đáp án D
Đặt ![]() theo giả thiết ta có:
theo giả thiết ta có:
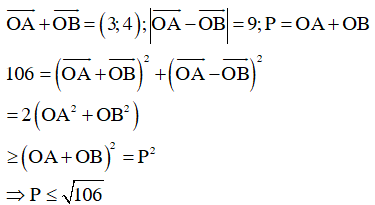
Tổng quát: Với 2 số thực thõa mãn ![]()
Khi đó ![]()
Câu 14:
Cho số phức z=2-3i. Số phức liên hợp của z là:
Đáp án C
Phương pháp: Số phức z=a+bi có số phức liên hợp
Cách giải: Số phức liên hợp của z=2-3i là
Câu 15:
Cho số phức . Tìm số phức được
Đáp án A
Phương pháp: Sử dụng công thức cộng, nhân các số phức.
Cách giải:
Câu 16:
Cho số phức z thỏa mãn . Mô đun của z là:
Đáp án C
Phương pháp: Đặt ![]() tính toán và rút gọn, so sánh hai số phức.
tính toán và rút gọn, so sánh hai số phức.
Cách giải:Gọi ![]() ta có:
ta có:

Câu 17:
Cho số phức z thỏa mãn điều kiện .
Tìm giá trị lớn nhất của biểu thức
Đáp án D
Phương pháp: Đưa biểu thức T về dạng biểu thức vector bằng cách tìm các vecto biểu diễn cho các số phức.
Cách giải:
Tập hợp các điểm z thỏa mãn điều kiện ![]() là đường tròn (C) tâm I(1;0) bán kính R=
là đường tròn (C) tâm I(1;0) bán kính R=
![]()
Gọi M là điểm biểu diễn cho số phức z, A(0;-1) là điểm biểu diễn cho số phức -i, B(2;1) là điểm biểu diễn cho số phức 2+i
Dễ thấy A,BC và ![]()
![]() AB là đường kính của đường tròn (C)
AB là đường kính của đường tròn (C)
![]() vuông tại M
vuông tại M
![]()
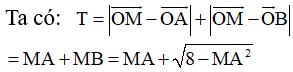
Đặt ![]()
Xét hàm số ![]() trên
trên ![]() ta có:
ta có:
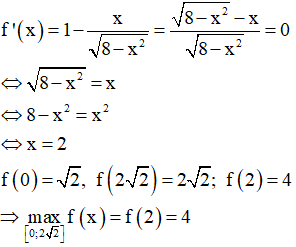
Vậy maxT=4
Câu 18:
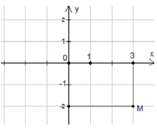
Cho số phức z có biểu diễn hình học là điểm M ở hình vẽ bên. Khẳng định nào sau đây đúng ?
Đáp án D
Phương pháp: Số phức z=a+bi được biểu diễn bởi điểm M(a;b) trên mặt phẳng phức.
Cách giải: Ta có: M(3;-2) z=3-2i
Câu 20:
Cho i là đơn vị ảo. Gọi S là tập hợp các số nguyên dương n có 2 chữ số thỏa mãn là số nguyên dương. Số phần tử của S là
Đáp án A
Phương pháp giải:
Để là số nguyên dương thì n là số nguyên dương chia hết cho 4
Lời giải:
Xét n=2k khi đó ![]() là số nguyên dương khi k chẵn.
là số nguyên dương khi k chẵn.
Kết hợp với ![]() suy ra
suy ra 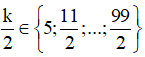 và
và ![]() là số chẵn.
là số chẵn.
Với mỗi bộ số 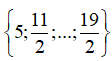 có 2 số k thỏa mãn,
có 2 số k thỏa mãn, 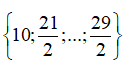 có 3 số k thỏa mãn.
có 3 số k thỏa mãn.
Vậy có tất cả 2.5+3.4=22 số thỏa mãn yêu cầu bài toán.
Câu 21:
Cho số phức z=-3+4i. Môđun của z là
Đáp án D
Phương pháp giải: Số phức z=a+bi có môđun là ![]()
Lời giải: Ta có ![]()
Câu 22:
Cho số phức z=(1+2i)(5-i), z có phần thực là
Đáp án B
Phương pháp: Số phức ![]() có phần thực là a, phần ảo là b.
có phần thực là a, phần ảo là b.
Cách giải:
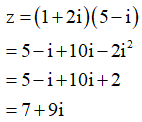
z có phần thực là 7.
Câu 23:
Số phức z thỏa mãn và số phức Tìm
Đáp án A
Phương pháp: Cho là hai số phức bất kì, khi đó ![]()
Cách giải: Ta có:
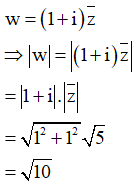
Câu 24:
Trong các số phức: số phức nào là số thực?
Đáp án B
Phương pháp:
Sử dụng ![]()
Cách giải:
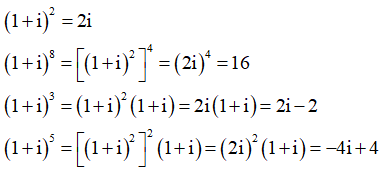
Như vậy, chỉ có số phức ![]() là số thực
là số thực
Câu 25:
Xét số phức z thỏa mãn . Mệnh đề nào dưới đây đúng?
Đáp án D
Phương pháp:
Chuyển vế, lấy mođun hai vế.
Cách giải: