Tính môđun số phức nghịch đảo của số phức z =
A.
B.
C.
D
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án D.
Ta có: ![]()
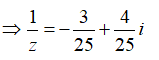
Từ đó suy ra
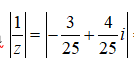
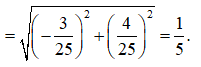
Cho số phức z = a + bi(a,b) thỏa mãn z + 2 + i - |z|(i+1) = 0 và |z| > 1. Tính P = a + b
Cho số phức z thỏa mãn |z - 3 - 4i| = . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = - . Tính mô đun của số phức = M + mi
Xét các số phức z = a + bi(a,b) thỏa mãn điều kiện |z - 4 - 3i| = . Tính P = a + b khi giá trị biểu thức |z + 1 - 3i + |z - 1 + i|| đạt giá trị lớn nhất.
Trên mặt phẳng phức tập hợp các số phức z = x + yi thỏa mãn |z + 2 - i| = | - 3i| là đường thẳng có phương trình
Cho các số phức với 0. Tập hợp các điểm biểu diễn số phức w = là đường tròn tâm là gốc tọa độ và bán kính bằng 1. Tập hợp các điểm biểu diễn số phức z là đường nào sau đây?
Cho số phức z và số phức liên hợp của nó có điểm biểu diễn là M, M’. Số phức z(4+3i) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức |z + 4i -5|
Gọi là bốn nghiệm phức của phương trình - 8 = 0. Trên mặt phẳng tọa độ z gọi A , B , C , D lần lượt là bốn điểm biểu diễn bốn nghiệm đó. Tính giá trị của P = OA + OB + OC + OD, trong đó O là gốc tọa độ.
Kí hiệu là nghiệm phức có phần thực âm và phần ảo dương của phương trình + 2z + 10 = 0. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức w = ?
Cho số phức z thỏa mãn điều kiện (1+i) - 1 - 3i = 0. Tìm phần ảo của số phức w = 1 - zi +
Cho A, B là hai điểm biểu diễn hình học số phức theo thứ tự khác 0 và thỏa mãn đẳng thức . Hỏi ba điểm O, A, B tạo thành tam giác gì? (O là gốc tọa độ)? Chọn phương án đúng và đầy đủ nhất.
Cho số phức z = a + bi(trong đó a, b là các số thực) thỏa mãn 3z - (4+5i) = -17 + 11i. Tính ab
Cho số phức z = a + bi(a,b). Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R = 3 . Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F = 4a + 3b -1. Tính giá trị M + m
Tìm giá trị lớn nhất của P = | - z| + | + z + 1| với z là số phức thỏa mãn |z| = 1