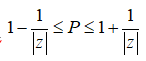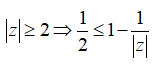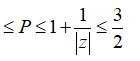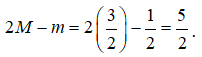225 Bài tập Số phức ôn thi Đại học có lời giải (P8)
-
5520 lượt thi
-
24 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho số phức z thỏa mãn: |z - 1 + i| = 2. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z là:
Đáp án C
Cách 1: Số phức z được biểu diễn bởi điểm M(x;y).
Số phức z1 được biểu diễn bởi điểm A(1;-1).
Em có: |z - 1 + i| = 2 => MA = 2
Vậy tập hợp điểm M là đường tròn tâm A(1;-1), bán kính R = 2 và có phương trình: ![]()
Cách 2: Đặt ![]() . Số phức z được biểu diễn bởi điểm M(x;y).
. Số phức z được biểu diễn bởi điểm M(x;y).
Em có:
![]()
![]()
![]()
Vậ tập hợp điểm M là đường tròn tâm I(1;-1), bán kính R = 2 và có phương trình: ![]()
Câu 2:
Cho 2 số phức z1 và z2 thỏa mãn: |z1 - 5 - i| = 3|z2 + 5 - 2i| = |iz2 - 3|. Giá trị nhỏ nhất của biểu thức P = |z1 - z2| là:
Đáp án D
Đặt ![]() Số phức z được biểu diễn bởi điểm
Số phức z được biểu diễn bởi điểm ![]()
Đặt![]() Số phức z2 được biểu diễn bởi điểm
Số phức z2 được biểu diễn bởi điểm ![]()
Suy ra: |z1 - z2| = MN
Em có: ![]()
![]()
Vậy điểm M thuộc đường tròn ![]() có tâm là điểm I(5;1) bán kính R = 3
có tâm là điểm I(5;1) bán kính R = 3
Em có
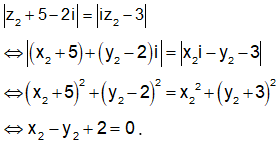
Vậy điểm N thuộc đường thẳng d: x - y + 2 = 0.
Dễ thấy đường thẳng d và đường tròn C không cắt nhau.
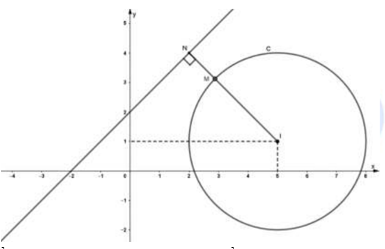
Áp dụng bất đẳng thức tam giác cho bộ ba điểm I, M, N em có:
![]()
![]()
Dấu “=” bằng xảy ra khi và chỉ khi I, M, N thẳng hàng và N là hình chiếu của I trên đường thẳng d.
Vậy ![]()
Câu 3:
Cho số phức z = a + bi(a,b) thỏa mãn z + 2 + i - |z|(i+1) = 0 và |z| > 1. Tính P = a + b
Đáp án D
Đặt z = a + bi
![]()
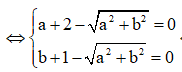
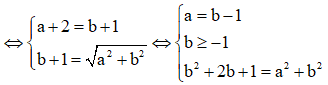
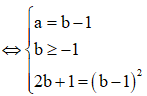
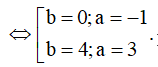
![]()
Câu 4:
Xét các số phức z = a + bi(a,b) thỏa mãn điều kiện |z - 4 - 3i| = . Tính P = a + b khi giá trị biểu thức |z + 1 - 3i + |z - 1 + i|| đạt giá trị lớn nhất.
Đáp án A
Gọi M(x;y) là điểm biều diễn số phức z.
Từ giả thiết, ta có |z - 4 - 3i| = 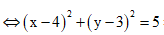
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R =
Khi đó P = MA + MB với A(-1;3), B(1;-1)
Ta có ![]()
Gọi E(0;1) là trung điểm của AB ![]()
Do đó ![]() mà
mà ![]() suy ra
suy ra ![]()
Với C là giao điểm của đường thẳng EI với đường tròn (C)
Vậy ![]() Dấu “=”xảy ra
Dấu “=”xảy ra 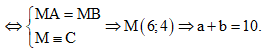
Câu 5:
Cho số phức z thỏa mãn điều kiện (1+i) - 1 - 3i = 0. Tìm phần ảo của số phức w = 1 - zi +
Đáp án C
giả sử ![]()
The giả thiết, ta có
![]()
![]()
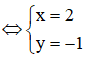
Suy ra ![]()
Ta có ![]()
![]()
Vậy chọn phần ảo là – 1
Câu 6:
Cho số phức z = a + bi(a,b) biết . Tính giá trị biểu thức P = a - b
Đáp án C
Đặt ![]() mà
mà ![]()
Suy ra ![]()
![]()
![]()
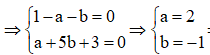
=> a - b = 3.
Câu 7:
Cho số phức z và số phức liên hợp của nó có điểm biểu diễn là M, M’. Số phức z(4+3i) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức |z + 4i -5|
Đáp án A
Giả sử ![]()
Ta có M(a;b) và M'(a;-b)
Khi đó ![]()
Suy ra ![]() và
và ![]()
Do 4 điểm M, N, M’, N’ tạo thành hình thang cân nhận Ox làm trục đối xứng nên 4 điểm đó lập thành hình chữ nhật
![]()
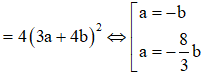
Với a = -b, ta có
![]()
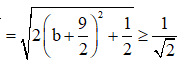
Dấu bằng xảy ra khi 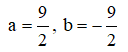
Với 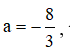 ta có
ta có 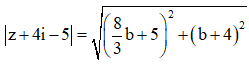
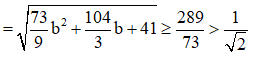
Vậy 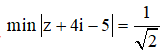
Câu 8:
Gọi là bốn nghiệm phức của phương trình - 8 = 0. Trên mặt phẳng tọa độ z gọi A , B , C , D lần lượt là bốn điểm biểu diễn bốn nghiệm đó. Tính giá trị của P = OA + OB + OC + OD, trong đó O là gốc tọa độ.
Đáp án D
![]()
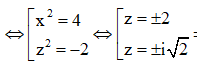
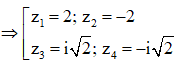
Khi đó ![]()
![]()
Câu 9:
Kí hiệu là nghiệm phức có phần thực âm và phần ảo dương của phương trình + 2z + 10 = 0. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức w = ?
Đáp án C
Ta có 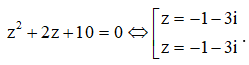
Suy ra ![]()
![]()
Suy ra điểm M(-3;-1) biểu diễn số phức w
Câu 10:
Cho số phức z = a + bi(a,b). Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R = 3 . Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F = 4a + 3b -1. Tính giá trị M + m
Đáp án B
Ta có phương trình đường tròn (C): ![]()
Do điểm A nằm trên đường tròn (C) nên ta có: ![]()
Mặt khác F = 4a + 3b -1 = 4(a-4) + 3(b-3) + 24
![]()
Ta có: ![]()
![]() = 25.9 = 255
= 25.9 = 255
![]()
![]()
Khi đó M = 39, m = 9
Vậy M + m = 48
Cách 2:
Ta có
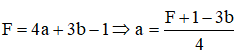
![]()
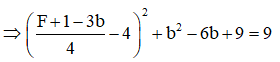
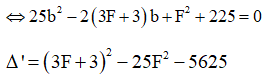
![]()
![]()
Câu 12:
Có bao nhiêu số phức z thỏa mãn |z| = |z + | = 1?
Đáp án C.
Đặt z = x + yi. Ta có:
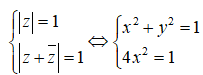
Hệ phương trình có bốn cặp nghiệm hay có tất cả bốn số phức z thỏa mãn.
Câu 13:
Tập hợp các điểm biểu diễn số phức z thỏa mãn 2|z-1| = |z + + 2| trên mặt phẳng tọa độ là một
Đáp án C.
Đặt z = x + yi. Ta có: 2|z-1| = |z + + 2|
![]()
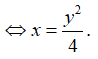
Câu 14:
Tìm giá trị lớn nhất của P = | - z| + | + z + 1| với z là số phức thỏa mãn |z| = 1
Đáp án C.
Với z = a + bi(a,b ), ta có:
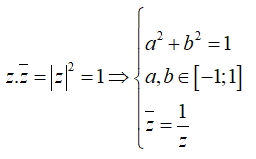
Do đó biến đổi ta được:

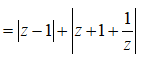
![]()
![]()
![]()
Khảo sát hàm ![]() trên đoạn [-1;1] ta được:
trên đoạn [-1;1] ta được:
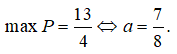
Câu 15:
Cho số phức z = a + bi(trong đó a, b là các số thực) thỏa mãn 3z - (4+5i) = -17 + 11i. Tính ab
Đáp án A
Có ![]()
![]() = -17 + 11i
= -17 + 11i
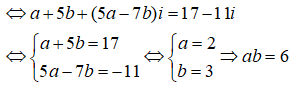
Câu 16:
Tổng các nghiệm phức của phương trình = 0 là
Đáp án B
Phương trình: = 0
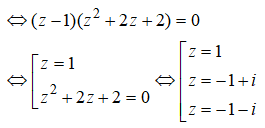
Tổng các nghiệm phức của phương trình đã cho là
![]()
Câu 17:
Trên mặt phẳng phức tập hợp các số phức z = x + yi thỏa mãn |z + 2 - i| = | - 3i| là đường thẳng có phương trình
Đáp án D
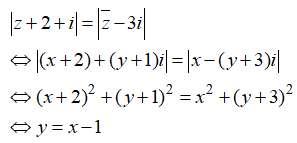
Câu 18:
Cho số phức z thỏa mãn |z - 3 - 4i| = . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = - . Tính mô đun của số phức = M + mi
Đáp án A
Đặt z = x + yi
Có ![]()
TH1:
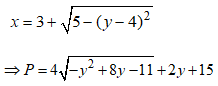
Xét hàm số: ![]() trên
trên ![]()
Có
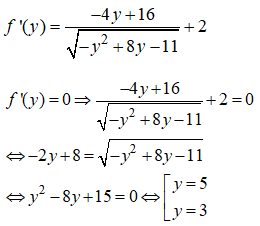
Ta có:
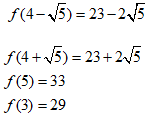
TH2:
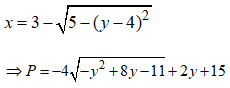
Xét hàm số: ![]() trên
trên ![]()
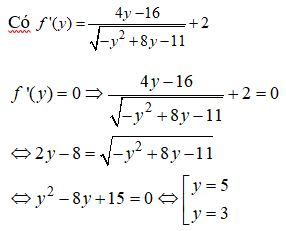
Ta có:
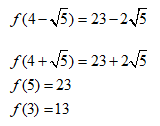
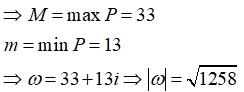
Câu 19:
Có bao nhiêu số phức z thỏa mãn:
Đáp án B
Gọi A1,A2 là điểm biểu diễn của số phức 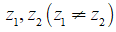 thì tập hợp những điểm M biểu diễn số phức z thỏa mãn
thì tập hợp những điểm M biểu diễn số phức z thỏa mãn
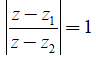 là đường trung trực của đoạn thẳng . Tìm ra z = 1 + i
là đường trung trực của đoạn thẳng . Tìm ra z = 1 + i
Câu 20:
Cho các số phức với 0. Tập hợp các điểm biểu diễn số phức w = là đường tròn tâm là gốc tọa độ và bán kính bằng 1. Tập hợp các điểm biểu diễn số phức z là đường nào sau đây?
Đáp án B
Ta có
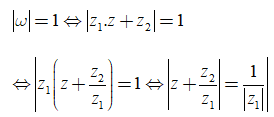
Câu 21:
Cho số phức z = a + bi(a,b ) và xét hai số phức . Trong các khẳng định dưới đây, khẳng định nào đúng?
Đáp án A
![]()
![]()
Câu 22:
Cho số phức z = a + bi(a,b ∈ℝ) thỏa mãn a + (b-1)i = . Giá trị nào dưới đây là mô đun của z?
Đáp án D
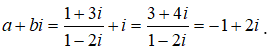
Từ đó ta có ![]()
Câu 23:
Cho A, B là hai điểm biểu diễn hình học số phức theo thứ tự khác 0 và thỏa mãn đẳng thức . Hỏi ba điểm O, A, B tạo thành tam giác gì? (O là gốc tọa độ)? Chọn phương án đúng và đầy đủ nhất.
Đáp án C
Với ta có ![]()
![]()
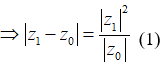
Với , ta có ![]()
![]()
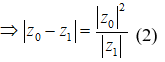
Từ (1), (2) ta có: 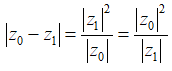
![]()
=> OA = OB = AB => OAB là tam giác đều.

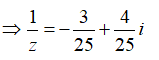
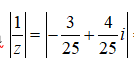
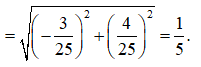
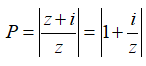 và
và 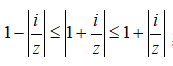 nên
nên