Cho tập A = {3;4;5;6}. Tìm số các số tự nhiên có bốn chữ số được thành lập từ tập A sao cho trong mỗi số tự nhiên đó, hai chữ số 3 và 4 mỗi chữ số có mặt nhiều nhất 2 lần, còn hai chữ số 5 và 6 mỗi chữ số có mặt không quá 1 lần.
A. 24
B. 30
C. 102
D. 360
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Chọn C
Ta có thể chia làm bốn trường hợp sau
TH1: Số 5 có mặt một lần, số 6 có mặt một lần.( Bao gồm các khả năng sau: mỗi số có mặt một lần hoặc một số 5, một số 6 hai số 3 hoặc một số 5, một số 6 hai số 4)
Số các số được tạo thành là: 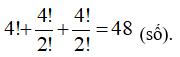
TH2: Số 5 có mặt một lần, số 6 không có mặt.
Số các số được tạo thành là: 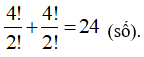
TH3: Số 6 có mặt một lần, số 5 không có mặt.
Số các số được tạo thành là: 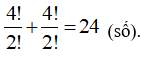
TH4: Số 5 và số 6 không có mặt.( Số 3 và số 4 mỗi số có mặt đúng hai lần)
Số các số được tạo thành là: 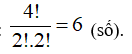
Vậy có thể lập được 102 số thỏa mãn đề bài.
Số cách xếp 4 học sinh vào một dãy ghế dài gồm 10 ghế, mỗi ghế chỉ một học sinh ngồi bằng
Có bao nhiêu cách xếp chỗ ngồi cho 4 bạn học sinh vào dãy có 4 ghế?
Có bao nhiêu số tự nhiên có 4 chữ số được viết từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 sao cho số đó chia hết cho 15?
Nhãn mỗi chiếc ghế trong một hội trường gồm hai phần : phần đầu là một chữ cái ( trong bảng 24 chữ cái tiếng Việt ), phần thứ hai là một số nguyên dương nhỏ hơn 26. Hỏi có nhiều nhất bao nhiêu chiếc ghế được ghi nhãn khác nhau ?
Có bao nhiêu cách chọn ra một tổ trưởng và một tổ phó từ một tổ có 10 người? Biết khả năng được chọn của mỗi người trong tổ là như nhau.
Một tổ có 10 học sinh. Số cách chọn ra hai bạn học sinh làm tổ trưởng và tổ phó là:
Một tổ học sinh có 5 học sinh nam và 7 học sinh nữ. Có bao nhiêu cách chọn 4 học sinh của tổ để tham ra một buổi lao động?
Cho trước 5 chiếc ghế xếp thành một hàng ngang. Số cách xếp ba bạn A, B, C vào 5 chiếc ghế đó sao cho mỗi bạn ngồi một ghế là
Lấy ngẫu nhiên một số tự nhiên có 9 chữ số khác nhau. Tính xác suất để số đó chia hết cho 3.
Một công việc để hoàng thành bắt buộc phải trải qua hai bước, bước thứ nhất có m cách thực hiện và bước thứ hai có n cách thực hiện. Số cách để hoàn thành công việc đã cho bằng
Kí hiệu là số tổ hợp chập k của n phần tử (0 k n). Mệnh đề nào sau đây đúng?