20 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Phương trình lượng giác nâng cao (P1)

Câu 1:

Tìm tập xác định của hàm số sau: y = $\frac{\tan 2 x}{sinx + 1}$ + $\cot (3 x + \frac{π}{6})$

A. R\{k $\frac{π}{2}$ , k ∈ Z}

B. R\{ $\frac{π}{2}$ + kπ, k ∈ Z}

C. R\{ $- \frac{π}{2}$ + k2π, k ∈ Z}

D. Tất cả sai

Xem đáp án

Đáp án D

Câu 2:

Tìm tập xác định của hàm số: y = $\frac{\tan 5 x}{\sin 4 x - \cos 3 x}$

A. R\{ $\frac{π}{10}$ + k $\frac{π}{5}$ , k ∈ Z)

B. R\{ $\frac{π}{2}$ + k2π, k ∈ Z)

C. R\{ $\frac{3 π}{14}$ + k $\frac{2 π}{7}$ , k ∈ Z)

D. Cả A; B; C đúng

Xem đáp án

Đáp án D

Điều kiện:

Câu 3:

Tập xác định của hàm số: y = $\frac{cotx}{\cos x - 1}$

A. R\{ k $\frac{π}{2}$ , k ∈ Z)

B. R\{ $\frac{π}{2}$ + kπ, k ∈ Z)

C. R\{ kπ, k ∈ Z)

D. R

Xem đáp án

Đáp án C

Câu 4:

Hàm số y = $\frac{2 - \sin 2 x}{\sqrt{m cosx + 1}}$ có tập xác định R khi

A. m > 0

B. 0 < m < 1

C. m ≠ -1

D. -1 < m < 1

Xem đáp án

Đáp án D

Hàm số có tập xác định R khi m cosx + 1 > 0, ∀x (*) .

Khi m = 0 thì (*) luôn đúng nên nhận giá trị m = 0.

Khi m > 0 thì mcosx + 1 ∈ [-m + 1; m + 1] nên (*) đúng khi -m + 1 > 0 => 0 < m < 1.

Khi m < 0 thì mcosx + 1 ∈ [m + 1; -m + 1] nên (*) đúng khi m + 1 > 0 => -1 < m < 0

Vậy giá trị m thoả mãn là -1 < m < 1.

Câu 5:

Tìm tập xác định của hàm số sau y = $\frac{\tan 2 x}{\sqrt{3} \sin 2 x - \cos 2 x}$

A.

B.

C.

D.

Xem đáp án

Đáp án A

Câu 6:

Trong các hàm số sau, có bao nhiêu hàm số là hàm chẵn trên tập xác định của nó?

y = cot 2x; y = cos(x + π); y = 1 – sin x; y = tan²⁰¹⁶x

A. 1.

B. 2

C. 3

D. 4

Xem đáp án

Đáp án B

+ Xét hàm y = f(x) = cos (x + π)

TXĐ: D = R

Với mọi x ∈ D, ta có: -x ∈ D và f(-x) = cos (-x + π) = -cos x = cos (x + π) = f(x)

Do đó y = cos (x + π) là hàm số chẵn .

+ Xét hàm y = g(x) = tan²⁰¹⁶x

TXĐ: D = R\{π/2 + kπ, k ∈ Z}

Với mọi x ∈ D, ta có: -x ∈ D và g(-x) = tan²⁰¹⁶(-x) = (-tan x)²⁰¹⁶ = tan²⁰¹⁶x = g(x)

Do đó: y = tan²⁰¹⁶x là hàm chẵn trên tập xác định của nó.

+Xét hàm y = cot2x

f(-x) = cot(-2x) = - cot 2x = -f(x) nên đây là hàm số lẻ.

+ Xét hàm số y = 1-sinx

f(-x) = 1- sin(-x) = 1+ sin x

Nên hàm số không chẵn không lẻ

Câu 7:

Xét tính chẵn lẻ của hàm số y = f(x) = cos(2x + $\frac{π}{4}$ ) + sin(2x - $\frac{π}{4}$ ), ta được

A. Hàm số chẵn.

B. Hàm số lẻ.

C. Không chẵn không lẻ.

D. Vừa chẵn vừa lẻ.

Xem đáp án

Đáp án D

Ta có tập xác định D = R.

Hàm số y = f(x) = 0 có:

f(-x) = 0 và –f(x) = 0

=> f(x) = f(-x) = -f(x) vừa thỏa mãn tính chất của hàm số chẵn, vừa thỏa mãn tính chất của hàm số lẻ, nên đây là hàm số vừa chẵn vừa lẻ.

Câu 8:

Trong các hàm số dưới đây có bao nhiêu hàm số là hàm số chẵn:

y = cos 3x (1); y = sin (x² + 1) (2) ;

y = tan² x (3); y = cot x (4);

A. 1 .

B. 2

C. 3 .

D. 4

Xem đáp án

Đáp án C.

+ Xét hàm y = f(x) = cos 3x

TXĐ: D = R

Với mọi x ∈ D, ta có: -x ∈ Dvà f(-x) = cos (-3x) = cos 3x = f(x)

Do đó, y = f(x) = cos 3x là hàm chẵn trên tập xác định của nó.

+ Xét hàm y = g(x) = sin (x² + 1)

TXĐ: D = R

Với mọi x ∈ D, ta có: -x ∈ D và g(-x) = sin ((-x)² + 1) = sin (x² + 1) = g(x)

Do đó: y = g(x) = sin (x² + 1) là hàm chẵn trên R.

+ Xét hàm y = h(x) = tan² x

TXĐ: D = R \ {π / 2 + kπ, k ∈ Z)

Với mọi x ∈ D, ta có: -x ∈ D và h(-x) = tan² (-x) = tan² x = h(x)

Do đó: y = h(x) = tan² x là hàm số chẵn trên D

+ Xét hàm y = t(x) = cot x.

TXĐ: D = R \ {kπ, k ∈ Z)

Với mọi x ∈ D, ta có: -x ∈ D và t(-x) = cot (-x) = -cot x = -t(x)

Do đó: y = t(x) = cot x là hàm số lẻ trên D.

Câu 9:

Cho hai hàm số f(x) = $\frac{1}{x - 3} + 3 \sin^{2} x$ và g(x) = $\sin \sqrt{1 - x}$ . Kết luận nào sau đây đúng về tính chẵn lẻ của hai hàm số này?

A. Hai hàm số là hai hàm số lẻ.

B. Hàm số f(x) là hàm số chẵn; hàm số g(x) là hàm số lẻ.

C. Hàm số f(x) là hàm số lẻ; hàm số g(x) là hàm số không chẵn không lẻ.

D. Cả hai hàm số đều là hàm số không chẵn không lẻ.

Xem đáp án

Đáp án D

a, Xét hàm số $f (x) = \frac{1}{x - 3} + 3 \sin^{2} x$ có tập xác định là D = R\{3}.

Ta có x = -3 ∈ D nhưng -x = 3 ∉ D nên D không có tính đối xứng. Do đó ta có kết luận hàm số f(x) không chẵn không lẻ.

b, Xét hàm số $g (x) = \sin \sqrt{1 - x}$ có tập xác định là D₂ = [1; + ∞). Dễ thấy D₂ không phải là tập đối xứng nên ta kết luận hàm số g(x) không chẵn không lẻ.

Câu 10:

Xét sự biến thiên của hàm số y = 1 - sinx trên một chu kì tuần hoàn của nó. Trong các kết luận sau, kết luận nào sai?

A. Hàm số đã cho nghịch biến trên khoảng ( $- \frac{π}{2}$ ; 0)

B. Hàm số đã cho nghịch biến trên khoảng (0; $\frac{π}{2}$ )

C. Hàm số đã cho đồng biến trên khoảng ( $\frac{π}{2}$ ; π)

D. Hàm số đã cho nghịch biến trên khoảng ( $\frac{π}{2}$ ; $\frac{3 π}{2}$ )

Xem đáp án

Đáp án D

Hàm số đã cho tuần hoàn với chu kỳ 2 $π$ và kết hợp với các phương án đề bài thì ta sẽ xét sự biến thiên của hàm số trên (-π/2; 3π/2)

Ta có hàm số y = sin x

* Đồng biến trên khoảng (-π/2; π/2)

* Nghịch biến trên khoảng (π/2; 3π/2)

Từ đây suy ra hàm số y = 1 - sinx

* Nghịch biến trên khoảng (-π/2; π/2)

* Đồng biến trên khoảng (π/2; 3π/2)

Câu 11:

Xét sự biến thiên của hàm số y = sinx - cosx. Trong các kết luận sau, kết luận nào đúng?

A. Hàm số đã cho đồng biến trên khoảng ( $- \frac{π}{4}$ ; $\frac{3 π}{4}$ )

B. Hàm số đã cho đồng biến trên khoảng ( $\frac{3 π}{4}$ ; $\frac{7 π}{4}$ )

C. Hàm số đã cho có tập giá trị là [-1; 1]

D. Hàm số đã cho luôn nghịch biến trên khoảng ( $- \frac{π}{4}$ ; $\frac{7 π}{4}$ )

Xem đáp án

Đáp án A

Ta có $y = \sin x - \cos x = \sqrt{2} \sin (x - \frac{π}{4})$

Từ đây ta có thể loại đáp án C, do tập giá trị của hàm số là $[- \sqrt{2}; \sqrt{2}]$

Hàm số đã cho tuần hoàn với chu kỳ 2π do vậy ta xét sự biến thiên của hàm số trên đoạn (-π/4; 7π/4)

Ta có:

* Hàm số đồng biến trên khoảng (-π/4; 3π/4)

* Hàm số nghịch biến trên khoảng (3π/4; 7π/4)

Câu 12:

Xét tính tuần hoàn và tìm chu kì (nếu có) của hàm số sau: y = cosx + cos( $\sqrt{3}$ x)

A: hàm số không tuần hoàn

B: Hàm số tuần hoàn với T = 2π

C: Hàm số tuần hoàn với T = π

D: Tất cả sai

Xem đáp án

Đáp án A

Câu 13:

Cho hàm số y = $\frac{1}{sinx}$ . Tìm mệnh đề đúng

A: hàm số không tuần hoàn

B: Hàm số tuần hoàn với T = 2π

C: Hàm số tuần hoàn với T = π

D: không xác định được chu kì.

Xem đáp án

Đáp án B

Câu 14:

Xét sự biến thiên của hàm số y = sinx - cosx. Tìm kết luận nào đúng?

A. Hàm số đã cho đồng biến trên khoảng ( $- \frac{π}{4}$ ; $\frac{3 π}{4}$ )

B. Hàm số đã cho đồng biến trên khoảng ( $\frac{3 π}{4}$ ; $\frac{7 π}{4}$ )

C. Hàm số đã cho có tập giá trị là [-1; 1]

D. Hàm số đã cho luôn nghịch biến trên khoảng ( $- \frac{π}{4}$ ; $\frac{7 π}{4}$ )

Xem đáp án

Đáp án A

Câu 15:

Xét hai mệnh đề sau:

(I) $\forall x \in (π, \frac{3 π}{2})$ : Hàm số y = $\frac{1}{\sin x}$ giảm

(II) $\forall x \in (π, \frac{3 π}{2})$ : Hàm số y = $\frac{1}{\cos x}$ giảm

Mệnh đề đúng trong hai mệnh đề trên là:

A. Chỉ (I) đúng

B. Chỉ (II) đúng.

C. Cả 2 sai

D. Cả 2 đúng

Xem đáp án

Đáp án B

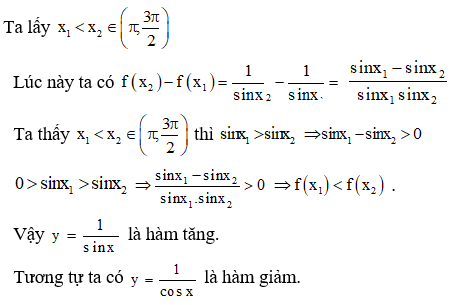
Câu 16:

Cho hàm số y = 4sin(x + $\frac{π}{6}$ ) cos(x - $\frac{π}{6}$ ) - sin2x. Kết luận nào sau đây là đúng về sự biến thiên của hàm số đã cho?

A. Hàm số đã cho đồng biến trên các khoảng (0; $\frac{π}{4}$ ) và ( $\frac{3 π}{4}$ ; π)

B. Hàm số đã cho đồng biến trên (0; π).

C. Hàm số đã cho nghịch biến trên khoảng (0; $\frac{3 π}{4}$ )

D. Hàm số đã cho đồng biến trên khoảng (0; $\frac{π}{4}$ ) và nghịch biến trên khoảng ( $\frac{π}{4}$ ; π)

Xem đáp án

Đáp án A

Ta có y = 4sin (x + π/6) cos (x - π/6) - sin 2x

= 2 (sin 2x + sin π/3) - sin 2x = sin 2x + $\sqrt{3}$

Xét sự biến thiên của hám số y = sin 2x + $\sqrt{3}$ ,

Ta thấy với A. Trên (0; π/4) thì giá trị của hàm số luôn tăng.

Tương tự trên (3π/4; π) thì giá trị của hàm số cũng luôn tăng.

Câu 17:

Tập xác định của hàm số y = tan( $\frac{π}{2} \cos x$ ) là:

A. R\{0;}

B. R\{0; π}

C. R\{k $\frac{π}{2}$ }

D. R\{kπ}

Xem đáp án

Đáp án D

Câu 18:

Hàm số y = sinx + cosx tăng trên khoảng nào?

A. ( $- \frac{3 π}{4}$ + k2π; $\frac{π}{4}$ + k2π)

B. ( $- \frac{3 π}{4}$ + kπ; $\frac{π}{4}$ + kπ)

C. ( $- \frac{π}{2}$ + k2π; $\frac{π}{2}$ + k2π)

D. (π + k2π; 2π + k2π)

Xem đáp án

Đáp án A

Câu 19:

Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?

A. $y = \frac{1}{\sin^{3} x}$

B. $y = \sin (x + \frac{π}{4})$

C. $y = \sqrt{2} \cos (x - \frac{π}{4})$

D. $y = \sqrt{\sin 2 x}$

Xem đáp án

Đáp án A

+ Phương án A: TXĐ: $x = R \ {k π}$

Ta có:

Nên hàm số này là hàm số lẻ; nhận gốc tọa độ làm tâm đối xứng.

+ Xét phương án B:

Do đó, hàm số này không là hàm chẵn, không là hàm lẻ.

+ Xét phương án C:

y= t(x) = sinx + cosx

suy ra: t(- x )= sin (- x) + cos (- x) = - sinx + cosx

do đó hàm số này không chẵn, không lẻ

Câu 20:

Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. y = 2cos(x + $\frac{π}{2}$ ) + sin(π - 2x)

B. y = sin (x - $\frac{π}{4}$ ) + sin (x + $\frac{π}{4}$ )

C. y = $\sqrt{2}$ sin (x + $\frac{π}{4}$ ) - sin x

D. $y = \sqrt{sinx} + \sqrt{cosx}$

Xem đáp án

Đáp án C

+ Xét phương án A: Tập xác định D = R

f(x) = -2sinx + sin 2x

f(- x) = - 2sin (-x) + sin (- 2x ) = 2sinx - sin2x

suy ra: f(- x)= - f(x) nên đây là hàm số lẻ

+ Xét phương án B: Tập xác định D= R.

$g (x) = \sqrt{2} . \sin x; g (- x) = \sqrt{2} . \sin (- x) = - \sqrt{2} . \sin x$

suy ra, g(- x) = - g(x) nên đây là hàm số lẻ

+ Xét phương án C: y = t(x) = cosx đây là hàm số chẵn

Chọn C

CHỌN BỘ SÁCH BẠN MUỐN XEM

100 câu trắc nghiệm Hàm số lượng giác nâng cao

100 câu trắc nghiệm Phương trình lượng giác nâng cao (P1)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương