Cho đa giác đều 20 cạnh. Lấy ngẫu nhiên 3 đỉnh của đa giác đều. Xác suất để 3 đỉnh lấy được là 3 đỉnh của một tam giác vuông không có cạnh nào là cạnh của đa giác đều bằng
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Chọn C
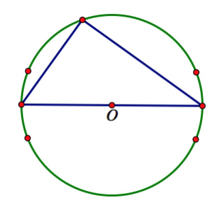
Đa giác đều nội tiếp một đường tròn tâm O. Lấy ngẫu nhiên 3 đỉnh có cách.
Để 3 đỉnh là 3 đỉnh một tam giác vuông không có cạnh nào là cạnh của đa giác đều thực hiện theo các bước:
Lấy một đường kính qua tâm đường tròn có 10 cách ta được 2 đỉnh.
Chọn đỉnh còn lại trong 20 - 2 - 4 = 14 đỉnh (loại đi 2 đỉnh thuộc đường kính và 4 đỉnh gần ngay đường kính đó) cách.
Vậy có tất cả 10.14 = 140 tam giác thoả mãn.
Xác suất cần tính bằng 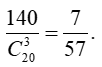
Có hai dãy ghế đối diện nhau, mỗi dãy có 5 ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam và 5 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất để mỗi học sinh nam đều ngồi đối diện một học sinh nữ.
Có 8 người khách bước ngẫu nhiên vào một cửa hàng có 3 quầy. Tính xác suất để 3 người cùng đến quầy thứ nhất.
Cho tập hợp S = {1,2,3...,17} gồm 17 số nguyên dương đầu tiên. Chọn ngẫu nhiên 3 phần tử của tập S. Tính xác suất để tập hợp con chọn được có tổng các phần tử chia hết cho 3.
Một hộp đựng 15 quả cầu trong đó có 6 quả màu đỏ, 5 quả màu xanh, 4 quả màu vàng. Lấy ngẫu nhiên 6 quả cầu trong 15 quả cầu đó. Tính xác suất để 6 quả lấy được có đủ ba màu.
Từ một hộp chứa 11 quả cầu màu đỏ và 4 quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác suất để lấy được 3 quả cầu màu xanh bằng
Một đoàn tàu gồm ba toa đỗ sân ga. Có 5 hành khách lên tàu. Mỗi hành khách độc lập với nhau. Chọn ngẫu nhiên một toa. Tìm xác suất để mỗi toa có ít nhất 1 hành khách bước lên tàu.
Có hai hộp chứa các quả cầu. Hộp thứ nhất chứa 7 quả cầu đỏ và 5 quả cầu màu xanh, hộp thứ hai chứa 6 quả cầu đỏ và 4 quả cầu màu xanh. Lấy ngẫu nhiên từ một hộp 1 quả cầu. Xác suất sao cho hai quả lấy ra cùng màu đỏ.
Trong một hộp có 3 bi đỏ, 5 bi xanh và 7 bi vàng. Bốc ngẫu nhiên 4 viên. Xác suất để bốc được đủ 3 màu là
Có hai hộp đựng bi, mỗi viên bi chỉ mang một màu trắng hoặc đen. Lấy ngẫu nhiên từ mỗi hộp đúng một viên bi. Biết tổng số bi ở hai hộp là 20 và xác suất để lấy được hai viên bi đen là . Tính xác suất để lấy được hai viên bi trắng.
Trong một phòng học, có 36 cái bàn rời nhau được đánh số từ 1 đến 36, mỗi bàn dành cho 1 học sinh. Các bàn được xếp thành một hình vuông có kích thước 6x6. Cô giáo xếp tuỳ ý 36 học sinh của lớp vào các bàn, trong đó có hai bạn A và B. Xác suất để A và B ngồi ở hai bàn xếp cạnh nhau bằng (theo chiều ngang hoặc chiều dọc).
Có hai dãy ghế đối diện nhau, mỗi dãy có năm ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam và 5 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ và bất kì hai học sinh ngồi liền kề nhau thì khác phái bằng
Gọi S là tập tất cả các số tự nhiên có bốn chữ số khác nhau. Chọn ngẫu nhiên một số từ tập S, tính xác suất để số được chọn lớn hơn số 6700.
Sắp ngẫu nhiên 5 học sinh nam và học sinh nữ thành một hàng ngang. Tính xác suất để không có học sinh nữ nào đứng cạnh nhau.
Một người đang đứng tại gốc O của trục tọa độ Oxy. Do say rượu nên người này bước ngẫu nhiên sang trái hoặc sang phải trên trục tọa độ với độ dài mỗi bước bằng 1 đơn vị. Xác suất để sau 10 bước người này quay lại đúng gốc tọa độ O bằng
Đội văn nghệ của một lớp có 5 bạn nam và 7 bạn nữ. Chọn ngẫu nhiên 5 bạn tham gia biểu diễn, xác suất để trong 5bạn được chọn có cả nam và nữ, đồng thời số nam nhiều hơn số nữ bằng