Cho hàm số ,∆x là số gia của đối số tại x. Khi đó ∆y/∆x bằng:
A.
B.
C.
d.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
![]()
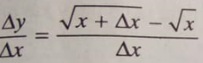
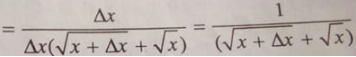
Chọn D
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng -1 là:
Cho biết điện lượng truyền trong dây dẫn theo thời gian biểu thị bởi hàm số , trong đó t được tính bằng giây (s) và Q được tính theo Culong (C). Tính cường độ dòng điện tại thời điểm t=4s.
Cho hàm số , có ∆x là số gia của đối số tại x=2. Khi đó ∆y/∆x bằng:
Cho hàm số . Để hàm số này có đạo hàm tại x= 2 thì giá trị của b là
Cho hàm số ,có ∆x là số gia của đối số tại x=1, ∆y là số gia tương ứng của hàm số. Khi đó ∆y bằng:
Cho hàm số:
Phương trình tiếp tuyến của (C) tại điểm A(1, (-1)/2) là:
Một chất điểm chuyển động thẳng có phương trình (t là thời gian tính bằng giây (s), S là đường đi tính bằng mét). Tính vận tốc (m/s) của chất điểm tại thời điểm to = 5(s)
Cho hàm số . Khi đó đạo hàm của hàm số tại điểm x = 0 là kết quả nào sau đây?