Cho parabol (P): và đường thẳng d: . Gọi A, B là các giao điểm của (P) và d. Tìm tọa độ điểm C trên trục tung cho CA + CB có giá trị nhỏ nhất.
A. C(; 0)
B. C(0; )
C. C(; 0)
D. C(0; -)
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án B
Hoành độ của A và B là nghiệm của phương trình
Phương trình này có hai nghiệm: x = 4 và x =
Suy ra A(4; 4), B()
Dễ thấy hai điểm A, B cùng nằm về một phía so với trục tung (do cùng có hoành độ dương).
Lấy điểm A’( −4; 4) đối xứng với A qua trục tung
Khi đó CA + CB = CA’ + CBA’B, nên CA + CB đạt giá trị nhỏ nhất khi và chỉ khi A’, C, B thẳng hàng, tức là khi C là giao điểm của đường thẳng A’B với trục tung.
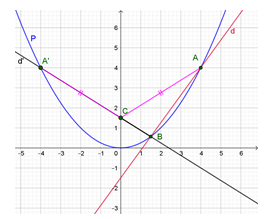
Phương trình đường thẳng d’ đi qua A’ và B có dạng y = ax + b
Cho Parabol (P): y = và đường thẳng (d): y = mx + 4. Biết đường thẳng (d) luôn cắt đồ thị (P) tại hai điểm phân biệt A, B. Gọi là hoành độ của các điểm A, B. Tìm giá trị lớn nhất của
Gọi là hai nghiệm của phương trình 2 – (3a – 1)x – 2 = 0. Tìm giá trị nhỏ nhất của biểu thức: P = + 2
Trong mặt phẳng Oxy cho đường thẳng (d): y = kx + và parabol (P): . Giả sử đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B. Tọa độ trung điểm M của đoạn thẳng AB luôn thỏa mãn phương trình nào dưới đây?
Trong mặt phẳng tọa độ Oxy cho Parabol (P): y = và đường thẳng (d): (m là tham số). Trong trường hợp (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ giao điểm là . Đặt f (x) = + (m + 1) – x khi đó?
Cho phương trình – (m + 1)x – 3 = 0 (1), với x là ẩn, m là tham số. Gọi là hai nghiệm của phương trình (1). Đặt B = . Tìm m khi B đạt giá trị lớn nhất.
Trên parabol (P): y = ta lấy ba điểm phân biệt A (a; ); B (b; ); C (c; ) thỏa mãn – b = – c = – a. Hãy tính tích T = (a + b + 1)(b + c + 1)(c + a + 1)
Trong mặt phẳng Oxy, cho parabol (P): y = và đường thẳng (d): x – 2y + 12 = 0. Gọi giao điểm của (d) và (P) là A, B. Tìm tọa độ điểm C nằm trên (P) sao cho tam giác ABC vuông tại C.
Giả sử phương trình bậc hai a + bx + c = 0 có hai nghiệm thuộc [0; 3]. Tìm giá trị lớn nhất của biểu thức: