20 câu hỏi trắc nghiệm thuộc Trắc nghiệm Ôn tập chương IV có đáp án (Phần 2)

Câu 1:

Gọi $x_{1}; x_{2}$ là hai nghiệm của phương trình 2 $x^{2}$ – (3a – 1)x – 2 = 0. Tìm giá trị nhỏ nhất của biểu thức: P = $\frac{3}{2}$ ${(x_{1} - x_{2})}^{2}$ + 2

A. 24

B. 20

C. 21

D. 23

Xem đáp án

Câu 2:

Giả sử phương trình bậc hai a $x^{2}$ + bx + c = 0 có hai nghiệm thuộc [0; 3]. Tìm giá trị lớn nhất của biểu thức: $Q = \frac{18 a^{2} - 9 ab + b^{2}}{9 a^{2} - 3 ab + ac}$

A. 5

B. 4

C. 2

D. 3

Xem đáp án

Đáp án D

Vì phương trình bậc hai có 2 nghiệm nên a $\neq$ 0. Biểu thức Q có dạng đẳng cấp bậc hai, ta chia cả tử và mẫu của Q cho $a^{2}$ thì $Q = \frac{18 - 9 \frac{b}{a} + {(\frac{b}{a})}^{2}}{9 - \frac{b}{a} + \frac{c}{a}}$

Gọi $x_{1}; x_{2}$ là hai nghiệm của phương trình, theo Vi-ét ta có: $\{\begin{cases} x_{1} + x_{2} = - \frac{b}{a} \\ x_{1} x_{2} = \frac{c}{a} \end{cases}$

Vậy giá trị lớn nhất của Q là 3

Câu 3:

Cho phương trình $x^{2}$ – (m + 1)x – 3 = 0 (1), với x là ẩn, m là tham số. Gọi $x_{1}; x_{2}$ là hai nghiệm của phương trình (1). Đặt B = $\frac{3 x_{1}^{2} + 3 x_{2}^{2} + 4 x_{1} + 4 x_{2} - 5}{x_{1}^{2} + x_{2}^{2} - 4}$ . Tìm m khi B đạt giá trị lớn nhất.

A. $\frac{- 1}{2}$

B. −1

C. 2

D. $\frac{1}{2}$

Xem đáp án

Đáp án A

Vậy giá trị lớn nhất của b bằng 7 khi $\frac{- 1}{2}$

Câu 4:

Cho Parabol (P): y = $x^{2}$ và đường thẳng (d): y = mx + 4. Biết đường thẳng (d) luôn cắt đồ thị (P) tại hai điểm phân biệt A, B. Gọi $x_{1}; x_{2}$ là hoành độ của các điểm A, B. Tìm giá trị lớn nhất của $Q = \frac{2 (x_{1} + x_{2}) + 7}{{x_{1}}^{2} + {x_{2}}^{2}}$

A. −1

B. $\frac{- 1}{2}$

C. 1

D. $\frac{1}{4}$

Xem đáp án

Đáp án C

Phương trình hoành độ giao điểm của (d) và (P) là: $x^{2}$ = mx + 4 <=> $x^{2}$ − mx − 4 = 0. Ta có $∆$ = $m^{2}$ + 16 > 0, với mọi m nên phương trình luôn có 2 nghiệm phân biệt, suy ra đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt.

Suy ra giá trị lớn nhất của Q là 1 khi m = 1

Câu 5:

Gọi $x_{A}, x_{B}$ là hoành độ của A và B. Tìm giá trị nhỏ nhất của biểu thức $T = \frac{4}{x_{A} + x_{B}} + \frac{1}{x_{A} . x_{B}}$

A. $\sqrt{2}$ + 1

B. 2

C. 2 $\sqrt{2}$

D. $\sqrt{2}$

Xem đáp án

Câu 6:

Trong mặt phẳng tọa độ Oxy cho Parabol (P): y = $x^{2}$ và đường thẳng (d): $y = - \frac{2}{3} (m + 1) x + \frac{1}{3}$ (m là tham số). Trong trường hợp (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ giao điểm là $x_{1}; x_{2}$ . Đặt f (x) = $x^{3}$ + (m + 1) $x^{2}$ – x khi đó?

A. $f (x_{1}) - f (x_{2}) = {(x_{1} - x_{2})}^{3}$

B. $f (x_{1}) - f (x_{2}) = {\frac{1}{2} (x_{1} - x_{2})}^{3}$

C. $f (x_{1}) - f (x_{2}) = {- (x_{1} - x_{2})}^{3}$

D. $f (x_{1}) - f (x_{2}) = {- \frac{1}{2} (x_{1} - x_{2})}^{3}$

Xem đáp án

Đáp án D

Xét phương trình hoành độ giao điểm của (d) và (P) ta có: $x^{2} = \frac{- 2 (m + 1)}{3} + \frac{1}{3} \Leftrightarrow$ 3 $x^{2}$ + 2(m + 1)x – 1 = 10 (1)

Ta thấy phương trình (1) có hệ số a và c trái dấu nên luôn có hai nghiệm phân biệt mọi m nên (P) và (d) luôn cắt nhau tại hai điểm phân biệt với mọi m

Theo hệ thức Vi-ét

Câu 7:

Trong mặt phẳng Oxy cho đường thẳng (d): y = kx + $\frac{1}{2}$ và parabol (P): $y = \frac{1}{2} x^{2}$ . Giả sử đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B. Tọa độ trung điểm M của đoạn thẳng AB luôn thỏa mãn phương trình nào dưới đây?

A. y = $x^{2} + \frac{1}{2}$

B. y = $x^{2}$

C. y = $x + \frac{1}{2}$

D. y = $\frac{1}{2} x$

Xem đáp án

Đáp án A

Xét phương trình hoành độ giao điểm của (d) và (P): $\frac{1}{2} x^{2}$ = kx + $\frac{1}{2}$ $\Leftrightarrow$ $x^{2}$ – 2kx – 1 = 0 (*). Nhận thấy a = 1;

c = −1 trái dấu nhau nên phương trình (*) luôn có hai nghiệm phân biệt hay đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A và B với mọi k

Gọi A( $x_{A}; y_{A}$ ); B( $x_{B}; y_{B}$ ) thì $x_{A}; x_{B}$ là hai nghiệm của phương trình (*) và

Câu 8:

Trên parabol (P): y = $x^{2}$ ta lấy ba điểm phân biệt A (a; $a^{2}$ ); B (b; $b^{2}$ ); C (c; $c^{2}$ ) thỏa mãn $a^{2}$ – b = $b^{2}$ – c = $c^{2}$ – a. Hãy tính tích T = (a + b + 1)(b + c + 1)(c + a + 1)

A. T = 2

B. T = 1

C. T = −1

D. T = 0

Xem đáp án

Câu 9:

Cho parabol (P): $y = \frac{1}{4} x^{2}$ và đường thẳng d: $y = \frac{11}{8} x - \frac{3}{2}$ . Gọi A, B là các giao điểm của (P) và d. Tìm tọa độ điểm C trên trục tung cho CA + CB có giá trị nhỏ nhất.

A. C( $\frac{3}{2}$ ; 0)

B. C(0; $\frac{3}{2}$ )

C. C( $\frac{1}{2}$ ; 0)

D. C(0; - $\frac{3}{2}$ )

Xem đáp án

Đáp án B

Hoành độ của A và B là nghiệm của phương trình $\frac{1}{4} x^{2} = \frac{11}{8} x - \frac{3}{2}$

Phương trình này có hai nghiệm: x = 4 và x = $\frac{3}{2}$

Suy ra A(4; 4), B( $\frac{3}{2}; \frac{9}{16}$ )

Dễ thấy hai điểm A, B cùng nằm về một phía so với trục tung (do cùng có hoành độ dương).

Lấy điểm A’( −4; 4) đối xứng với A qua trục tung

Khi đó CA + CB = CA’ + CB $\geq$ A’B, nên CA + CB đạt giá trị nhỏ nhất khi và chỉ khi A’, C, B thẳng hàng, tức là khi C là giao điểm của đường thẳng A’B với trục tung.

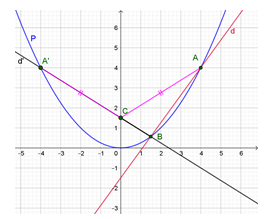
Phương trình đường thẳng d’ đi qua A’ và B có dạng y = ax + b

Câu 10:

Trong mặt phẳng Oxy, cho parabol (P): y = $\frac{1}{4} x^{2}$ và đường thẳng (d): x – 2y + 12 = 0. Gọi giao điểm của (d) và (P) là A, B. Tìm tọa độ điểm C nằm trên (P) sao cho tam giác ABC vuông tại C.

A. C (2; 1)

B. C (1; 2)

C. (1; 0)

D. (0; 2)

Xem đáp án

Đáp án A

Câu 11:

Để hệ phương trình $\{\begin{cases} x + y = S \\ x . y = P \end{cases}$ có nghiệm, điều kiện cần và đủ là:

A. $S^{2}$ – P < 0

B. $S^{2}$ – P $\geq$ 0

C. $S^{2}$ – 4P < 0

D. $S^{2}$ – 4P $\geq$ 0

Xem đáp án

Câu 12:

Hệ phương trình $\{\begin{cases} x^{2} + y^{2} = 4 \\ x + y = 2 \end{cases}$ có nghiệm là (x; y) với x > y. Khi đó xy bằng:

A. 0

B. 1

C. 2

D. 4

Xem đáp án

Câu 13:

Hệ phương trình $\{\begin{cases} x^{2} + y^{2} = 20 \\ x + y = 6 \end{cases}$ có nghiệm là (x; y) với x > y. Khi đó tổng 3x + 2y bằng:

A. 14

B. 10

C. 12

D. 16

Xem đáp án

Câu 14:

Hệ phương trình $\{\begin{cases} x . y + x + y = 11 \\ x^{2} y + {xy}^{2} = 30 \end{cases}$

A. Có 2 nghiệm (2; 3) và (1; 5)

B. Có 2 nghiệm (2; 1) và (3; 5)

C. Có 1 nghiệm là (5; 6)

D. Có 4 nghiệm là (2; 3); (3; 2); (1; 5); (5; 1)

Xem đáp án

Đáp án D

Vậy hệ phương trình có bốn nghiệm (2; 3); (3; 2); (1; 5); (5; 1)

Câu 15:

Hệ phương trình $\{\begin{cases} x^{2} y + {xy}^{2} = 6 \\ xy + x + y = 5 \end{cases}$

A. Có 2 nghiệm (5; 1) và (1; 5)

B. Có 2 nghiệm (2; 1) và (1; 2)

C. Có 1 nghiệm là (2; 2)

D. Có 4 nghiệm (1; 2); (2; 1); (1; 5) và (5; 1)

Xem đáp án

Đáp án B

Vậy hệ phương trình có hai nghiệm (1; 2) và (2; 1)

Câu 16:

Hệ phương trình $\{\begin{cases} x + y + xy = 5 \\ x^{2} + y^{2} = 5 \end{cases}$ có bao nhiêu nghiệm?

A. 0

B. 1

C. 2

D. 4

Xem đáp án

Đáp án C

Vậy hệ phương trình có hai nghiệm

Câu 17:

Hệ phương trình $\{\begin{cases} x + y + 2 xy = - 8 \\ x^{2} + y^{2} = 10 \end{cases}$ có bao nhiêu nghiệm?

A. 0

B. 1

C. 2

D. 4

Xem đáp án

Đáp án D

Câu 18:

Hãy chỉ ra các cặp nghiệm khác 0 của hệ phương trình $\{\begin{cases} x^{2} = 5 x - 2 y \\ y^{2} = 5 y - 2 x \end{cases}$

A. (3; 3)

B. (2; 2); (3; 1); (−3; 6)

C. (1; 1); (2; 2); (3; 3)

D. (−2; −2); (1; −2); (−6; 3)

Xem đáp án

Đáp án A

Trừ vế với vế của hai phương trình ta được:

Vậy nghiệm khác 0 của hệ là (3; 3)

Câu 19:

Hệ phương trình $\{\begin{cases} x^{2} = 3 x - y \\ y^{2} = 3 y - x \end{cases}$ có bao nhiêu cặp nghiệm (x; y)?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án B

Khi x = y thì $x^{2}$ – 2x = 0. Suy ra hoặc x = 0 => y = 0 hoặc x = 2 => y = 2

Khi y = 4 – x thì $x^{2}$ – 4x + 4 = 0 <=> x = 2 => y = 2

Vậy hệ phương trình có hai nghiệm là (0; 0), (2; 2)

Câu 20:

Các cặp nghiệm khác (0; 0) của hệ phương trình $\{\begin{cases} x^{2} = 3 x + 2 y \\ y^{2} = 3 y + 2 x \end{cases}$

A. (5; 5)

B. (5; 5), (1; −2), (−2; 1)

C. (5; 5), (1; 2), (2; 1)

D. (5; 5); (−1; 2), (2; −1)

Xem đáp án

Đáp án D

Trừ vế với vế của hai phương trình ta được:

Vậy nghiệm khác 0 của hệ là (5; 5); (−1; 2), (2; −1)

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Ôn tập chương IV có đáp án

Trắc nghiệm Ôn tập chương IV có đáp án (Phần 2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương