Một lớp học có 25 học sinh chơi bóng đá; 23 học sinh chơi bóng bàn; 14 học sinh chơi bóng đá và bóng bàn và 6 học sinh không chơi môn nào cả. Số học sinh của cả lớp là:

Lớp 10B có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Lý và Toán, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả Toán, Lý, Hóa. Số học sinh của  lớp 10B là:

Trong kì thi học sinh giỏi cấp trường, lớp 10A có 17 bạn được công nhận học sinh giỏi Văn, có 25 bạn được công nhận học sinh giỏi Toán. Biết cả lớp 10A có 45 học sinh và có 13 học sinh không đạt học sinh giỏi. Số học sinh giỏi cả Văn lẫn Toán là:

Chứng minh rằng: “Với mọi số tự nhiên n, n³ chia hết cho 3 thì n chia hết cho 3”. Một bạn học sinh đã dùng phản chứng như sau:

Bước 1: Giả sử n không chia hết cho 3 khi đó n = 3k + 1 hoặc n = 3k + 2, k ∈ N .

Bước 2: Với n = 3k + 1 ta có  n³ = (3k + 1)³ = 27k³ + 27k²  + 9k + 1 chia hết cho 3

Bước 3: Với n = 3k + 2 ta có  n³ = (3k + 2)³ = 27k³ + 54k² + 36k + 4 không chia hết cho 3 (mâu thuẫn)

Bước 4: Vậy n chia hết cho 3.

Lập luận trên sai từ bước nào?

Lớp 10A có 45 học sinh trong đó có 15 bạn được xếp lực học giỏi, 20 bạn được xếp hạnh kiểm tốt, có 10 bạn vừa được xếp lực học giỏi vừa được hạnh kiểm tốt. Số học sinh của lớp 10A được nhận khen thưởng là:

Có 60 học sinh giỏi, mỗi em giỏi ít nhất một môn. Có 22 em giỏi Văn, 25 em giỏi Toán, 20 em giỏi Anh. Có 8 em giỏi đúng 2 môn Văn, Toán; có 7 em giỏi đúng hai môn Toán, Anh; có 6 em giỏi đúng hai môn Anh, Văn. Số em giỏi cả ba môn Văn, Toán, Anh là:

Để phục vụ cho hội nghị quốc tế, ban tổ chức đã huy động 30 cán bộ phiên dịch tiếng Anh, 25 cán bộ phiên dịch tiếng Pháp, trong đó 12 cán bộ phiên dịch được cả 2 thứ tiếng Anh và Pháp. Ban tổ chức đã huy động tất cả bao nhiêu cán bộ phiên dịch cho hội nghị đó?

Chứng minh rằng: “Nếu phương trình bậc hai : ax² + bx + c = 0 vô nghiệm thì a và c cùng dấu”. Một học sinh đã làm như sau:

Bước 1: Giả sử phương trình vô nghiệm và a, c cùng dấu.

Bước 2: Với điều kiện a, c trái dấu ta có a.c > 0 suy ra Δ  = b² - 4ac > 0.

Bước 3: Nên phương trình có hai nghiệm phân biệt, điều này mâu thuẫn với giả thiết phương trình vô nghiệm.

Bước 4: Vậy phương trình vô nghiệm thì a, c phải cùng dấu.

Lập luận trên sai từ bước nào?

Một miếng đất hình chữ nhật có chiều rộng x = 43m ± 0,5m và chiều dài y = 63m ± 0,5m. Chu vi mảnh đất là

Cho A và B là hai tập hợp con của tập hợp E được biểu diễn bởi biểu đồ Ven dưới đây

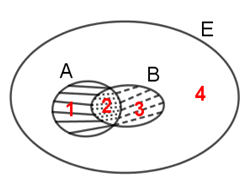
Trong các phát biểu sau

      I.            Vùng 1 là tập hợp A \ B.

     II.            Vùng 2 là tập hợp A ∩ B.

     III.            Vùng 3 là tập hợp B \ A.

       IV.            Vùng 4 là tập hợp E \ (A ∪  B).

Số phát biểu đúng là:

Các nhà khoa học Mỹ đang nghiên cứu liệu một máy bay có thể có tốc độ gấp bảy lần tốc độ ánh sáng. Với máy bay đó trong một năm (giả sử một năm có 365 ngày) nó bay được bao nhiêu? Biết vận tốc ánh sáng là 300 nghìn km/s. Kết quả dưới dạng kí hiệu khoa học là:

Viết dạng chuẩn của số gần đúng a biết a = 1,3462 sai số tương đối của a bằng 1%.

Biết rằng tốc độ của ánh sáng trong chân không là 300000km/s. Hỏi mỗi năm (365 ngày) ánh sáng đi được trong chân không là bao nhiêu? Viết dưới dạng kí hiệu khoa học.

Đo chiều dài của một cây cầu, ta được số đo a = 192,55m, với sai số tương đối không vượt quá 0,2%. Giá trị gần đúng của chiều dài cây cầu là:

“Chứng minh rằng $\sqrt{2}$  là số vô tỉ”. Một học sinh đã làm như sau:

Bước 1: Giả sử $\sqrt{2}$ là số hữu tỉ, tức là $\sqrt{2}$ = $\frac{m}{n}$, trong đó m, n ∈ N* , (m, n) = 1

Bước 2: Từ  $\sqrt{2}$ = $\frac{m}{n}$ => m² = 2n²   => m²  là số chẵn

=> m là số chẵn => m = 2k, k ∈ N*.

=> n²  = 2k²  => n²  là  số chẵn =>  n là số chẵn

Bước 3: Do đó m chẵn, n chẵn mâu thuẫn với (m, n) = 1.

Bước 4: Vậy $\sqrt{2}$ là số vô tỉ.

Lập luận trên đúng tới bước nào?

Cho số x  = $\frac{2}{7}$. Cho các giá trị gần đúng của  là 0,28; 0,29; 0,286. Giá trị gần đúng tốt nhất là: