Tập nghiệm của bất phương trình là:
A.
B.
C.
D.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án đúng là: A
Ta có: .
Bảng xét dấu
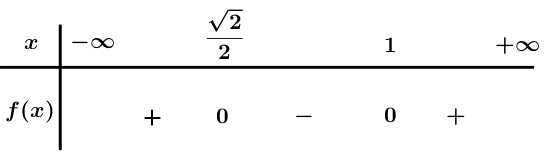
Dựa vào bảng xét dấu .
Cho bất phương trình . Trong các tập hợp sau đây, tập nào có chứa phần tử không phải là nghiệm của bất phương trình.