Cho tam giác ABC vuông tại A, kẻ tia phân giác $\widehat{ABC}$  cắt AC tại D.

a) Biết BC = 5cm, AB = 3 cm. Tính AC và AD.

b) Qua D kẻ DH vuông góc với BC tại H. Chứng minh ∆ABC  ∆HDC từ đó chứng minh CH.CB = CD.CA.

c) E là hình chiếu của A trên BC. Chứng minh $\frac{BC}{BA}=\frac{HC}{HE}$ .

d) O là giao điểm của BD và AH. Qua B kẻ đường thẳng song song với AH cắt các tia CO và CA lần lượt tại M và N. Chứng minh M là trung điểm của BN.

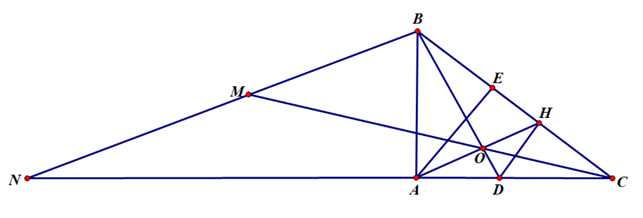
a) Ta có ∆ABC vuông tại A nên ta có:

AB² + AC² = BC² ( định lý Py – ta – go)

Þ AC² = BC² – AB² = 5² – 3² = 25 – 9 = 16

Þ AC = 4 (cm).

Xét ∆ABC có BD là tia phân giác của $\widehat{ABC}$  (D Î AC)

Ta có: $\frac{AD}{DC}=\frac{BA}{BC}$  (định lý)

Mà DC = BC – AD = 5 – AD

$\Rightarrow \frac{AD}{5-AD}=\frac{BA}{BC}=\frac{3}{5}$

Þ 5.AD = 3.(5 – AD)

Û 5AD = 15 – 3AD

Û 8AD = 15

Û AD =$\frac{15}{8}$ = 1,875 (cm)

Vậy độ dài đoạn AC là 4 cm và AD là 1,875 cm.

b) Theo đề ∆ABC vuông tại A nên có $\widehat{BAC}={90}^o$ ;

DH vuông góc với BC tại H nên $\widehat{DHC}={90}^o$ ;

Do đó $\widehat{BAC}=\widehat{DHC}={90}^o$ .

Xét ∆ABC và ∆HDC có:

$\widehat{BCA}$ chung (giả thiết)

$\widehat{BAC}=\widehat{DHC}={90}^o$(cmt)

Suy ra, ∆ABC $\backsim$  ∆HDC (g.g)

Vì ∆ABC $\backsim$  ∆HDC (cmt) nên $\frac{CH}{CA}=\frac{CD}{CB}$  (các cạnh tương ứng tỉ lệ)

Þ CH.CB = CA.CD.

c) Vì E là hình chiếu của A trên BC nên (E Î BC).

DH vuông góc với BC tại H (H Î BC).

Suy ra DH // AE (định lý)

Áp dụng định lý Ta – let trong ∆AEC có DH // AE (cmt)

Ta có: $\frac{HC}{HE}=\frac{DC}{DA}$  (1);

Xét ∆ABC có BD là tia phân giác của $\widehat{ABC}$  (D Î AC)

Ta có: $\frac{BC}{BA}=\frac{DC}{DA}$  (2);

Từ (1) và (2) suy ra $\frac{HC}{HE}=\frac{BC}{BA}=\frac{DC}{DA}$ .