Cho bốn điểm A, B, C, D trong đó không có ba điểm nào thẳng hàng, bất kì hai điểm nào cũng có khoảng cách lớn hơn 10. Chứng minh rằng tồn tại hai điểm đã cho có khoảng cách lớn hơn 14.

Trước hết ta chứng minh một bài toán phụ:

Cho $\Delta ABC, \widehat{A}\ge 90°$. Chứng minh rằng $B{C}^2\ge A{B}^2+A{C}^2$.

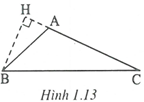
Vẽ $BH\perp AC$. Vì $\widehat{A}\ge 90°$ nên H nằm trên tia đối của tia AC.

Xét $\Delta HBC$ và $\Delta HBA$ vuông tại H, ta có:

$$\begin{gathered} B{C}^2=H{B}^2+H{C}^2=\left(A{B}^2-H{A}^2\right)+{\left(HA+AC\right)}^2 \\ =A{B}^2-H{A}^2+H{A}^2+A{C}^2+2HA.AC=A{B}^2+A{C}^2+2HA.AC \end{gathered}$$

Vì $HA.AC\ge 0$ nên $B{C}^2\ge A{B}^2+A{C}^2$ ( dấu “=” xảy ra khi $H\equiv A$ tức là khi  $\Delta ABC$vuông ).

Vận dụng kết quả trên để giải bài toán đã cho

Trường hợp tứ giác ABCD là tứ giác lồi (h.1.14)

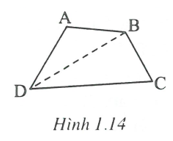
Ta có: $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$

Suy ra trong bốn góc này phải có một góc lớn hơn hoặc bằng $90°$, giả sử $\widehat{A}\ge 90°$

Xét $\Delta ABD$ ta có $B{D}^2\ge A{B}^2+A{D}^2>{10}^2+{10}^2=200$ suy ra $BD>\sqrt{200}$, do đó BD > 14

Trường hợp tứ giác ABCD là tứ giác lõm (h.1.15)

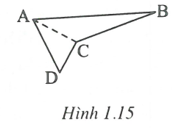
Nối CA, Ta có: $\widehat{ACD}+\widehat{ACB}+\widehat{BCD}=360°$.

Suy ra trong ba góc này phải có một góc lớn hơn hoặc bằng $120°$.

Giả sử $\widehat{ACB}\ge 120°$, do đó $\widehat{ACB}$ là góc tù

Xét $\Delta ACB$ có $A{B}^2\ge A{C}^2+B{C}^2>{10}^2+{10}^2=200$

Suy ra $AB>\sqrt{200}\Rightarrow AC>14$

Vậy luôn tồn tại hai điểm đã cho có khoảng cách lớn hơn 14.