9 câu hỏi trắc nghiệm thuộc Dạng 2. Tìm mối liên hệ giữa các cạnh, đường chéo của tứ giác có đáp án

Câu 1:

Cho tứ giác ABCD. Chứng minh:

a) Tổng hai cạnh đối nhỏ hơn tổng hai đường chéo;

Xem đáp án

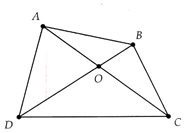
a) Sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác OAB, OBC,OCD và ODA.

Câu 2:

b) Tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy.

Xem đáp án

b) Chứng minh tổng hai đường chéo lớn hơn nửa chu vi tứ giác sử dụng kết quả của a).

Chứng minh tổng hai đường chéo nhỏ hơn chu vi tứ giác sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác ABC, ADC, ABD và CBD.

Câu 3:

Cho tứ giác ABCD và một điểm M thuộc miền trong của tứ giác. Chứng minh:

a) MA + MB + MC + MD ≥ AB + CD;

Xem đáp án

a) HS tự chứng minh

Câu 4:

b) MA + MB + MC + MD ≥

\frac{1}{2}

(AB + BC + CD + DA).

Xem đáp án

b) Tương tự 2A a)

Câu 5:

Có hay không một tứ giác mà độ dài các cạnh tỉ lệ với 1, 3, 5, 10 ?

Xem đáp án

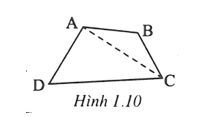
Giả sử tứ giác ABCD có CD là cạnh dài nhất.

Ta sẽ chứng minh CD nhỏ hơn tổng của ba cạnh còn lại (1).

Thật vậy, xét $Δ A B C$ ta có: $A C < A B + B C$

Xét $Δ A D C$ có: $C D < A D + A C$ . Do đó $C D < A D + A B + B C$ .

Ta thấy nếu các cạnh tỉ lệ với 1, 3, 5, 10 thì không thỏa mãn điều kiện (1) nên không có tứ giác nào mà các cạnh tỉ lệ với 1, 3, 5, 10.

Câu 6:

Tứ giác ABCD có hai đường chéo vuông góc. Biết AB = 3; BC = 6,6; CD = 6. Tính độ dài AD.

Xem đáp án

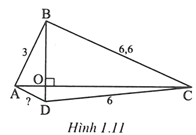
Gọi O là giao điểm của hai đường chéo.

Xét $Δ A O B; Δ C O D$ vuông tại O, ta có: $A B^{2} + C D^{2} = O A^{2} + O B^{2} + O C^{2} + O D^{2}$

Chứng minh tương tự, ta được: $B C^{2} + A D^{2} = O B^{2} + O C^{2} + O D^{2} + O A^{2}$

Do đó: $A B^{2} + C D^{2} = B C^{2} + A D^{2}$

Suy ra: $3^{2} + 6^{2} = 6, 6^{2} + A D^{2} \Rightarrow A D^{2} = 9 + 36 - 43, 56 = 1, 44 \Rightarrow A D = 1, 2$

Câu 7:

Chứng minh rằng trong một tứ giác tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác.

Xem đáp án

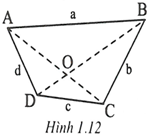
Gọi O là giao điểm của hai đường chéo AC và BD của tứ giác ABCD.

Gọi độ dài các cạnh AB, BC, CD, DA lần lượt là a, b, c, d.

Vận dụng bất đẳng thức tam giác ta được: $O A + O B > a; O C + O D > c$

Do đó $(O A + O C) + (O B + O D) > a + c$ hay $A C + B D > a + c$ (1)

Chứng minh tương tự, ta được: $A C + B D > d + b$ (2)

Cộng từng vế của (1) và (2), ta được:

$2 (A C + B D) > a + b + c + d \Rightarrow A C + B D > \frac{a + b + c + d}{2}$

Xét các $Δ A B C$ và $Δ A D C$ ta có: $A C < a + b; A C < c + d$

$\Rightarrow 2 A C < a + b + c + d$ (3)

Tương tự có: $2 B D < a + b + c + d$ (4)

Cộng từng vế của (3) và (4) được: $2 (A C + B D) < 2 (a + b + c + d)$

$\Rightarrow A C + B D < a + b + c + d$

Từ các kết quả trên ta được điều phải chứng minh.

Câu 8:

Cho bốn điểm A, B, C, D trong đó không có ba điểm nào thẳng hàng, bất kì hai điểm nào cũng có khoảng cách lớn hơn 10. Chứng minh rằng tồn tại hai điểm đã cho có khoảng cách lớn hơn 14.

Xem đáp án

Trước hết ta chứng minh một bài toán phụ:

Cho $Δ A B C, \hat{A} \geq 90 °$ . Chứng minh rằng $B C^{2} \geq A B^{2} + A C^{2}$ .

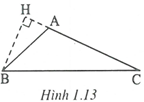
Cho bốn điểm A, B, C, D trong đó không có ba điểm nào thẳng hàng, bất kì hai điểm nào cũng có khoảng cách lớn hơn 10. (ảnh 1)

Vẽ $B H ⊥ A C$ . Vì $\hat{A} \geq 90 °$ nên H nằm trên tia đối của tia AC.

Xét $Δ H B C$ và $Δ H B A$ vuông tại H, ta có:

$B C^{2} = H B^{2} + H C^{2} = (A B^{2} - H A^{2}) + {(H A + A C)}^{2} = A B^{2} - H A^{2} + H A^{2} + A C^{2} + 2 H A . A C = A B^{2} + A C^{2} + 2 H A . A C$

Vì $H A . A C \geq 0$ nên $B C^{2} \geq A B^{2} + A C^{2}$ ( dấu “=” xảy ra khi $H \equiv A$ tức là khi $Δ A B C$ vuông ).

Vận dụng kết quả trên để giải bài toán đã cho

Trường hợp tứ giác ABCD là tứ giác lồi (h.1.14)

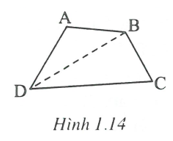
Cho bốn điểm A, B, C, D trong đó không có ba điểm nào thẳng hàng, bất kì hai điểm nào cũng có khoảng cách lớn hơn 10. (ảnh 2)

Ta có: $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360 °$

Suy ra trong bốn góc này phải có một góc lớn hơn hoặc bằng $90 °$ , giả sử $\hat{A} \geq 90 °$

Xét $Δ A B D$ ta có $B D^{2} \geq A B^{2} + A D^{2} > 10^{2} + 10^{2} = 200$ suy ra $B D > \sqrt{200}$ , do đó BD > 14

Trường hợp tứ giác ABCD là tứ giác lõm (h.1.15)

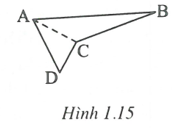
Cho bốn điểm A, B, C, D trong đó không có ba điểm nào thẳng hàng, bất kì hai điểm nào cũng có khoảng cách lớn hơn 10. (ảnh 3)

Nối CA, Ta có: $\hat{A C D} + \hat{A C B} + \hat{B C D} = 360 °$ .

Suy ra trong ba góc này phải có một góc lớn hơn hoặc bằng $120 °$ .

Giả sử $\hat{A C B} \geq 120 °$ , do đó $\hat{A C B}$ là góc tù

Xét $Δ A C B$ có $A B^{2} \geq A C^{2} + B C^{2} > 10^{2} + 10^{2} = 200$

Suy ra $A B > \sqrt{200} \Rightarrow A C > 14$

Vậy luôn tồn tại hai điểm đã cho có khoảng cách lớn hơn 14.

Câu 9:

Cho tứ giác ABCD có độ dài các cạnh là a , b , c , d đều là các số tự nhiên. Biết tổng S = a + b + c + d chia hết cho a , cho b , cho c , cho d . Chứng minh rằng tồn tại hai cạnh của tứ giác bằng nhau.

Xem đáp án

Cho tứ giác ABCD có độ dài các cạnh là a , b , c , d đều là các số tự nhiên. Biết tổng S = a + b + c + d chia hết cho (ảnh 1)

Ta chứng minh bằng phương pháp phản chứng.

Giả sử không có hai cạnh nào của tứ giác bằng nhau.

Ta có thể giả sử $a < b < c < d$ .

Ta có: $a + b + c > B D + c > d$

Do đó a + b + c + d > 2d . Ta đặt a + b + c + d = S thì S > 2d. (*)

Ta có:

$S ⋮ a \Rightarrow S = m a (m \in N)$ (1)

$S ⋮ b \Rightarrow S = n b (n \in N)$ (2)

$S ⋮ c \Rightarrow S = p c (p \in N)$ (3)

$S ⋮ d \Rightarrow S = q d (q \in N)$ (4)

Từ (4) và (*) => qd > 2d do đó q > 2

Vì a < b < c < d nên từ (1), (2), (3), (4) suy ra $m > n > p > q > 2$

Do đó $q \geq 3; p \geq 4; n \geq 5; m \geq 6$

Từ (1), (2), (3), (4) suy ra $\frac{1}{m} = \frac{a}{S}; \frac{1}{n} = \frac{b}{S}; \frac{1}{p} = \frac{c}{S}; \frac{1}{q} = \frac{d}{S}$

Ta có: $\frac{1}{6} + \frac{1}{5} + \frac{1}{4} + \frac{1}{3} \geq \frac{1}{m} + \frac{1}{n} + \frac{1}{p} + \frac{1}{q} = \frac{a + b + c + d}{S} = 1$

Từ đó: $\frac{19}{20} \geq 1$ ; vô lí.

Vậy điều giả sử là sai, suy ra tồn tại hai cạnh của tứ giác bằng nhau.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập Toán 8 Chủ đề 1: Tứ giác có đáp án

Dạng 2. Tìm mối liên hệ giữa các cạnh, đường chéo của tứ giác có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương