Câu hỏi:

22/07/2024 97

Cho tứ giác ABCD có $\hat{A} = \hat{C}$ tia phân giác góc B cắt đường thẳng AD ở M; tia phân giác của góc D cắt đường thẳng BC ở N. Chứng minh rằng: BM // CN

Xem lời giải

Bắt Đầu Thi Thử

Trả lời:

Giải bởi qa.haylamdo.com

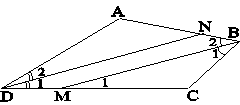
Xét tứ giác ABCD có: $\hat{B} + \hat{D} = 360^{o} - (\hat{A} + \hat{C}) = 360^{o} - 2 \hat{C} .$

Vì $\hat{B_{1}} = \hat{B_{2}}; \hat{D_{1}} = \hat{D_{2}}$ nên $\hat{B_{1}} + \hat{D_{1}} = 180^{o} - \hat{C}$

$\Rightarrow \hat{B_{1}} + \hat{D_{1}} + \hat{C} = 180^{o} .$ (1)

Xét $△$ BCM có $\hat{B_{1}} + \hat{M_{1}} + \hat{C} = 180^{o} .$ (2)

Từ (1) và (2) suy ra $\hat{D_{1}} = \hat{M_{1}} .$ Do đó BM // CN

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho tứ giác lồi ABCD có $\hat{B} + \hat{D} = 180^{0}; C B = C D$ . Chứng minh AC là tia phân giác của $\hat{B A D}$ .

Xem đáp án » 19/10/2022 596

Câu 2:

Cho tứ giác ABCD, $\hat{A} - \hat{B} = 50^{0} .$ Các tia phân giác của góc C và góc D cắt nhau tại O. Cho biết $\hat{C O D} = 115^{0} .$ Chứng minh rằng $A B ⊥ B C .$

Xem đáp án » 19/10/2022 300

Câu 3:

b) Gọi I là giao điểm của các tia phân giác của $\hat{A}$ và $\hat{B}$ của tứ giác. Chứng minh: $\hat{AIB} = \frac{\hat{C} + \hat{D}}{2}$

Xem đáp án » 19/10/2022 147

Câu 4:

Cho tứ giác ABCD biết $\hat{B} + \hat{C} = 200^{0}; \hat{B} + \hat{D} = 180^{0}; \hat{C} + \hat{D} = 120^{0}$

a) Tính số đo các góc của tứ giác.

Xem đáp án » 19/10/2022 82

Câu 5:

a) Có tứ giác nào có 4 góc nhọn không?

Xem đáp án » 19/10/2022 79

Câu 6:

Tứ giác ABCD có $\overset{⏜}{C} + \overset{⏜}{D} = 90^{0}$ . Chứng minh rằng ${AC}^{2} + {BD}^{2} = {AB}^{2} + {CD}^{2}$

Xem đáp án » 19/10/2022 79

Câu 7:

b) Cho tứ giác ABCD có $\hat{A} = 55^{0}; \hat{B} = 107^{0}; \hat{C} = 72^{0}$ . Tính số đo góc ngoài tại đỉnh D

Xem đáp án » 19/10/2022 74

Câu 8:

a) Cho tứ giác ABCD có $\hat{A} = 55^{0}; \hat{B} = 110^{0}; \hat{D} = 75^{0}$ . Tính số đo góc $\hat{C}$

Xem đáp án » 19/10/2022 73

Câu 9:

Cho tứ giác ABCD có O là giao điểm các tia phân giác của các góc C và D.

a) Tính $\hat{C O D}$ biết $\hat{A} = 120^{0}, \hat{B} = 90^{0}$

Xem đáp án » 19/10/2022 72

Câu 10:

Tứ giác ABCD có $\overset{⏜}{C} = 100^{0}, \overset{⏜}{D} = 60^{0}, \overset{⏜}{A} : \overset{⏜}{B} = 3 : 2$ . Tính các góc A và B.

Xem đáp án » 19/10/2022 71

Câu 11:

b) Một tứ giác có nhiều nhất bao nhiêu góc nhọn, bao nhiêu góc tù, bao nhiêu góc vuông?

Xem đáp án » 19/10/2022 69

Câu 12:

Cho tứ giác ABCD, M là một điểm trong tứ giác đó. Xác định vị trí của M để MA + MB + MC + MD nhỏ nhất.

Xem đáp án » 19/10/2022 66

Câu 13:

b) Tính $\hat{C O D}$ theo $\hat{A}$ và $\hat{B}$ .

Xem đáp án » 19/10/2022 62

Câu 14:

c) Các tia phân giác của góc A và B cắt nhau ở I và cắt các tia phân giác các góc C và D thứ tự ở E và F. Chứng minh rằng tứ giác OEIF có các góc đối bù nhau.

Xem đáp án » 19/10/2022 56

Xem thêm các câu hỏi khác »

Đề thi liên quan

Xem thêm »

Trắc nghiệm Toán 8 Nhân đơn thức với đa thức, đa thức với đa thức có lời giải chi tiết

2 đề 9086 lượt thi Thi thử
Bài tập Nhân đơn thức với đa thức (có lời giải chi tiết)

2 đề 6030 lượt thi Thi thử
Tổng hợp bài tập Toán 8 Chương 3: Phương trình bậc nhất một ẩn

13 đề 5073 lượt thi Thi thử
Top 12 Đề kiểm tra Toán 8 Học Kì 2 Chương 3 Đại Số có đáp án, cực hay

16 đề 4962 lượt thi Thi thử
Bài tập Những hằng đẳng thức đáng nhớ (có lời giải chi tiết)

2 đề 3665 lượt thi Thi thử
Top 8 Đề kiểm tra Toán 8 Học Kì 1 Chương 1 Hình học có đáp án, cực hay

9 đề 3565 lượt thi Thi thử
Đề thi Toán lớp 8 Giữa học kì 2 năm 2020 - 2021 có đáp án

10 đề 3539 lượt thi Thi thử
Top 8 Đề kiểm tra Toán 8 Học Kì 2 Chương 4 Đại Số có đáp án, cực hay

11 đề 2816 lượt thi Thi thử
Top 8 Đề kiểm tra Đại Số Toán 8 Học Kì 1 Chương 2 có đáp án, cực hay

9 đề 2795 lượt thi Thi thử
Top 11 Đề kiểm tra Đại số Toán 8 Học Kì 1 Chương 1 có đáp án, cực hay

6 đề 2761 lượt thi Thi thử

Xem thêm »

Hỏi bài

Câu hỏi mới nhất

Xem thêm »

3) Tính số đo các góc của $Δ D M N$ .

210 19/10/2022 Xem đáp án
2) Chứng minh: $Δ A M D = Δ B N D$ .

214 19/10/2022 Xem đáp án
Cho hình thoi ABCD có AB = BD. Gọi M, N lần lượt trên các cạnh AB, BC sao cho AM + NC = AD.

1) Chứng minh: AM = BN.

246 19/10/2022 Xem đáp án
3) Tổng độ dài (DM + DN) không đổi.

163 19/10/2022 Xem đáp án
2) $Δ A B M = Δ D B N$

175 19/10/2022 Xem đáp án
Cho hình thoi ABCD có $\hat{A} = 60 °$ . Một góc xBy thay đổi sao cho tia Bx cắt cạnh AD tại M, tia By cắt cạnh CD tại N và $\hat{x B y} = 60 °$ . Chứng minh :

1) AB = BD.

234 19/10/2022 Xem đáp án
4) Tính diện tích hình thoi ABCD.

168 19/10/2022 Xem đáp án
3) Biết chu vi của hình thoi ABCD là 8cm . Tính độ dài đường chéo BD ; AC.

169 19/10/2022 Xem đáp án
2) Gọi O là giao điểm của AC và BD. Chứng minh: $O A^{2} = \frac{3}{4} A B^{2}$ .

171 19/10/2022 Xem đáp án
Cho hình thoi ABCD có AB = BD.

1) Chứng minh: Tam giác ABD đều.

164 19/10/2022 Xem đáp án

Xem thêm »

CHỌN BỘ SÁCH BẠN MUỐN XEM

Câu hỏi:

Cho tứ giác ABCD có A^=C^ tia phân giác góc B cắt đường thẳng AD ở M; tia phân giác của góc D cắt đường thẳng BC ở N. Chứng minh rằng: BM // CN

Trả lời:

Xét tứ giác ABCD có: B^+D^=360o−A^+C^=360o−2C^. Vì B1^=B2^; D1^=D2^ nên B1^+D1^=180o−C^ ⇒B1^+D1^+C^=180o. (1) Xét △BCM có B1^+M1^+C^=180o. (2) Từ (1) và (2) suy ra D1^=M1^. Do đó BM // CN

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho tứ giác lồi ABCD có B^+D^=1800; CB=CD. Chứng minh AC là tia phân giác của BAD^.

Câu 2:

Cho tứ giác ABCD, A^−B^=500. Các tia phân giác của góc C và góc D cắt nhau tại O. Cho biết COD^=1150. Chứng minh rằng AB⊥BC.

Câu 3:

b) Gọi I là giao điểm của các tia phân giác của A^ và B^ của tứ giác. Chứng minh: AIB^=C^+D^2

Câu 4:

Cho tứ giác ABCD biết B^+C^=2000; B^+D^=1800; C^+D^=1200 a) Tính số đo các góc của tứ giác.

Câu 5:

a) Có tứ giác nào có 4 góc nhọn không?

Câu 6:

Tứ giác ABCD có C⏜+D⏜=900 . Chứng minh rằng AC2+BD2=AB2+CD2

Câu 7:

Cho tứ giác ABCD có $\hat{A} = \hat{C}$ tia phân giác góc B cắt đường thẳng AD ở M; tia phân giác của góc D cắt đường thẳng BC ở N. Chứng minh rằng: BM // CN

Cho tứ giác lồi ABCD có $\hat{B} + \hat{D} = 180^{0}; C B = C D$ . Chứng minh AC là tia phân giác của $\hat{B A D}$ .

Cho tứ giác ABCD, $\hat{A} - \hat{B} = 50^{0} .$ Các tia phân giác của góc C và góc D cắt nhau tại O. Cho biết $\hat{C O D} = 115^{0} .$ Chứng minh rằng $A B ⊥ B C .$

b) Gọi I là giao điểm của các tia phân giác của $\hat{A}$ và $\hat{B}$ của tứ giác. Chứng minh: $\hat{AIB} = \frac{\hat{C} + \hat{D}}{2}$

Cho tứ giác ABCD biết $\hat{B} + \hat{C} = 200^{0}; \hat{B} + \hat{D} = 180^{0}; \hat{C} + \hat{D} = 120^{0}$

a) Tính số đo các góc của tứ giác.

Tứ giác ABCD có $\overset{⏜}{C} + \overset{⏜}{D} = 90^{0}$ . Chứng minh rằng ${AC}^{2} + {BD}^{2} = {AB}^{2} + {CD}^{2}$