Dạng 4: Bài tập tự luyện có đáp án
-
546 lượt thi
-
15 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 2:
Câu 4:
Câu 6:
Cho tứ giác ABCD biết
a) Tính số đo các góc của tứ giác.
a) Từ giả thiết ta có:
Vì
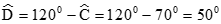
Câu 7:
Câu 8:
a) Tứ giác ABCD có
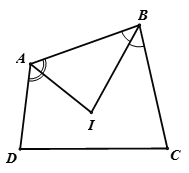
Câu 10:
c) Các tia phân giác của góc A và B cắt nhau ở I và cắt các tia phân giác các góc C và D thứ tự ở E và F. Chứng minh rằng tứ giác OEIF có các góc đối bù nhau.
c) Chứng minh tương tự như câu b, ta được
Do đó: . Suy ra:Câu 11:
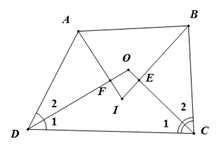
Xét có
(vì ).
Xét tứ giác ABCD có do đó
Vậy Theo đề bài nên
Mặt khác, nên Do đó
Câu 12:
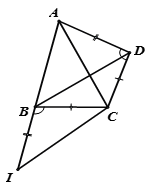
Trên tia đối tia BA lấy điểm I sao cho
Ta có (cùng bù với )
. Từ đó ta có .
Suy ra: và
Tam giác ACI cân tại C nên .
Vậy AC là phân giác trong
Câu 13:
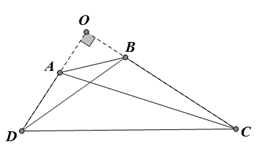
Gọi O là giao điểm AD và BC.
Ta có nên
Áp dụng định lí Py – ta – go,
Ta có
Nên
Câu 14:
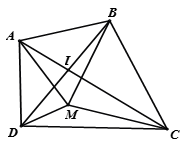
Gọi I là giao điểm của AC và BD. Ta có các bất đẳng thức:
Từ đó suy ra
khi M trùng với I.
Vậy khi M là giao điểm hai đường chéo thì nhỏ nhất.
Câu 15:
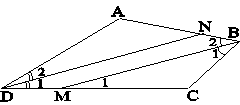
Xét tứ giác ABCD có:
Vì nên
(1)
Xét BCM có (2)
Từ (1) và (2) suy ra Do đó BM // CN
