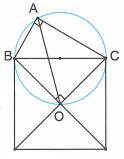
Trên cạnh huyền BC của tam giác vuông ABC về phía ngoài ta dựng hình vuông với tâm tại điểm O. Chứng minh rằng AO là tia phân giác của góc .
Giải bởi qa.haylamdo.com
Vì O là tâm của hình vuông nên .
Lại có suy ra bốn điểm cùng nằm trên đường tròn đường kính BC.
Đối với đường tròn này ta thấy (góc nội tiếp cùng chắn ).
Mà .
Do , nên .
Vậy , nghĩa là AO là tia phân giác của góc vuông (đpcm).
Cho tam giác ABC nội tiếp trong đường tròn (O). Đường phân giác trong góc A cắt đường tròn ngoại tiếp tam giác tại D. Gọi I là tâm đường tròn nội tiếp tam giác ABC. Chứng minh .
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Từ đỉnh A ta kẻ đường cao AH (H thuộc BC). Chứng minh rằng .
