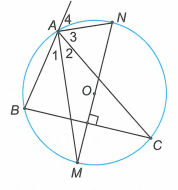
Cho tam giác nội tiếp trong đường tròn (O). Vẽ đường kính (điểm M thuộc cung BC không chứa A). Chứng minh rằng các tia AM, AN lần lượt là các tia phân giác trong và ngoài tại đỉnh A của tam giác ABC.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Vì nên M là điểm chính giữa của cung
. Do đó AM là tia phân giác của góc BAC.
Ta có: (góc nội tiếp chắn nửa đường tròn). (1)
. (2)
Từ (1) và (2) suy ra là tia phân giác của góc ngoài tại đỉnh A của tam giác ABC.
Cho nửa đường tròn (O) đường kính AB và dây AC căng cung AC có số đo bằng 60 độ.
a) So sánh các góc của tam giác ABC.
Cho tam giác ABC cân tại A( góc A < 90 độ). Vẽ đường tròn đường kính AB cắt BC tại D, cắt AC tại E. Chứng minh rằng:
a) Tam giác DBE cân.
c) Giả sử MA=12cm, MB=16cm, tính bán kính của đường tròn nội tiếp tam giác MAB
Cho tam giác ABC, vẽ đường tròn tâm O đi qua A và tiếp xúc với BC tại B. Kẻ dây BD song song với AC. Gọi I là giao điểm của CD với đường tròn.
Chứng minh .
b) Vẽ CH vuông góc với AB. Chứng minh rằng tia CM là tia phân giác của góc HCO.
Từ một điểm A ở bên ngoài đường tròn (O), ta vẽ hai cát tuyến ABC và ADE (B nằm giữa A và C; D nằm giữa A và E). Cho biết . Chứng minh .
Cho hai đường tròn và cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn cắt tại C và tiếp tuyến tại A của đường tròn cắt tại D.
Chứng minh .
Cho đường tròn (O) và một dây AB. Vẽ đường kính CD vuông góc với AB (D thuộc cung nhỏ AB). Trên cung nhỏ BC lấy một điểm N. Các đường thẳng CN và DN lần lượt cắt đường thẳng AB tại F và E. Tiếp tuyến của đường tròn (O) tại N cắt đường thẳng AB tại I. Chứng minh rằng:
a) Các tam giác INE và INF là tam giác cân.
Cho đường tròn (O) đường kính AB, M là điểm chính giữa của một nửa đường tròn. C là điểm bất kì trên nửa đường tròn kia, CM cắt AB tại D. Vẽ dây AE vuông góc với CM tại F.
a) Chứng minh rằng tứ giác ACEM là hình thang cân.
b) Gọi M là trung điểm BC. Chứng minh rằng ba điểm H,M,F thẳng hàng.
b) Gọi M, N lần lượt là điểm chính giữa của các cung AC và BC. Hai dây AN và BM cắt nhau tại I. Chứng minh rằng tia CI là tia phân giác của góc ACB.