Cho tam giác ABC vuông tại A. Kẻ đường cao AH và phân giác trong AD của góc HAC. Phân giác trong góc ABC cắt AH, AD lần lượt tại M, N. Chứng minh rằng BND = 90.
Giải bởi qa.haylamdo.com
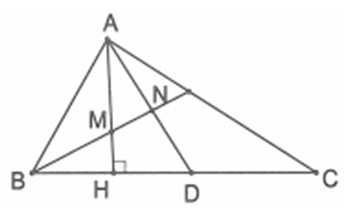
Ta có AMN = BMH = 90 - MBH, NDH = 90 - HAD mà MBH = ABC, HAD = HAC và ABC = HAC do cùng phụ với góc BCA, từ đó suy ra AMN = ADH hay tứ giác MHDN nội tiếp => MND = MHD = 90.
Cho nửa đường tròn tâm I, đường kính MN. Kẻ tiếp tuyến Nx và lấy điểm P chính giữa của nửa đường tròn. Trên cung PN, lấy điểm Q (không trùng với P, N ). Các tia MP và MQ cắt tiếp tuyến Nx theo thứ tự tại S và T.
a) Chứng minh NS = MN.
Cho tam giác ABC cân tại A và nội tiếp trong đường tròn tâm O, đường kính AI. Gọi E là trung điểm của AB, K là trung điểm của OI, H là trung điểm của EB.
a) Chứng minh HK AB.
